Surface area - high school - practice problems
Number of problems found: 259
- Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - A cone 3
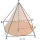 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - Cylinder 82991
 Please express r from the formula for the surface of the cylinder.
Please express r from the formula for the surface of the cylinder.
- Semicircle 82687
 If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it.
If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it. - Calculate 82567
 The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area.
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - Cylinder-shaped 81512
 A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have?
A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have? - Determine 81311
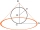 The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm.
The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm. - Dimensions 79294
 The swimming pool dimensions are as follows: l:w:h = 10:4:1. The pool can hold 625 m³ of water. Calculate how many square meters of tiles need to be purchased for lining the pool walls if we add 5% for waste.
The swimming pool dimensions are as follows: l:w:h = 10:4:1. The pool can hold 625 m³ of water. Calculate how many square meters of tiles need to be purchased for lining the pool walls if we add 5% for waste.
- A Pile of salt
 A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile?
A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile? - Calculate 74024
 The diagonal of the axial section of the rotating cylinder is 6 cm, and its surface is 30 cm square. Calculate the radius of the base.
The diagonal of the axial section of the rotating cylinder is 6 cm, and its surface is 30 cm square. Calculate the radius of the base. - An Elizabethan collar
 An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown.
An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown. - An equivalent
 An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h?
An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h? - Deviation 70434
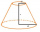 Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
- Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Original 63974
 If we reduce the length of the cube edge by 30%, this cube has a reduced surface area of 1176 cm². Find the edge length and volume of the original cube.
If we reduce the length of the cube edge by 30%, this cube has a reduced surface area of 1176 cm². Find the edge length and volume of the original cube. - Calculate 62864
 The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides.
The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides. - Side wall planes
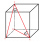 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Slant height 2
 A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
