Math word problems
Mathematical word problems allow you to practice your mathematics knowledge in everyday tasks. Word problems train to understand, translate into the mathematical language (e.g., equations), solve, and check the accuracy and solution discussion.
Choose a topic you want to calculate and improve in.
Choose a topic you want to calculate and improve in.
977surface area
719cuboid
531cube
520prism
453cylinder
255pyramid
229cone
218sphere
52frustum
4214equation
407divisibility
272sets
462probability
282variations
230permutations
637mean
34variance
2045multiplication
1793division
1524subtraction
1441addition
897square root
550comparing
457rounding
185cube root
164third power
3033length
2863area
2847time
2346volume
2238unit conversion
1842money
1386mass
1147angle
987velocity
570power
366density
290temperature
209acceleration
177energy
292sine
271tangent
266cosine
45arcsine
2501square
2321triangle
2129area of a shape
1619right triangle
952perimeter
941circle
925rectangle
514diagonal
268trapezoid
209polygon
180rhombus
71chord
46annulus
40rhomboid
21parabola
themes, topics
775work
165map scale
102Ohm's law
540line
164line segment
116vector
5891functions
1977percentages
1972reason
1469ratio
164maximum
123factorial
102minimum
76per mil
24modulo
3487fractions
1649natural numbers
320integers
159real numbers
41matrix
From our database of math word problems and examples, we offer the following:
- Nick was
 Nick was scuba diving at -32 1/2 feet. If he descends another 8 3/5 feet, what is his location?
Nick was scuba diving at -32 1/2 feet. If he descends another 8 3/5 feet, what is his location? - One-quarter 5440
 They delivered goods to four stores. First, they collected one-third of the shipment, second only two-thirds of what happened in the first. In the third, one-quarter of the rest, and the fourth, the remaining 240 kg. How much did they make at each store?
They delivered goods to four stores. First, they collected one-third of the shipment, second only two-thirds of what happened in the first. In the third, one-quarter of the rest, and the fourth, the remaining 240 kg. How much did they make at each store? - Determine 69364
 Determine the angle ϕ: ϕ + 71 ° 15 '= 90 °
Determine the angle ϕ: ϕ + 71 ° 15 '= 90 ° - The cup
 In a measuring cup set, the cup measure is 6 cm wide. The set also contains a 1-cup measure and a cup measure, both of which are similar in shape to the cup measure. Find the width of: a) 1/2 cup b) the 1 cup measure c) the 1/3 cup measure.
In a measuring cup set, the cup measure is 6 cm wide. The set also contains a 1-cup measure and a cup measure, both of which are similar in shape to the cup measure. Find the width of: a) 1/2 cup b) the 1 cup measure c) the 1/3 cup measure. - Ferdinand
 Ferdinand went from place A to place B and from there to place C. A is 7.2 km from B, and B is 11.7 km from C. Albert went from place A to place D and from there to place C. D is 9.1 km from A and C is 10.8 km from D. Who traveled more and by how much?
Ferdinand went from place A to place B and from there to place C. A is 7.2 km from B, and B is 11.7 km from C. Albert went from place A to place D and from there to place C. D is 9.1 km from A and C is 10.8 km from D. Who traveled more and by how much? - Theorem prove
 We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption do we start?
We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption do we start? - Two fractions multiply
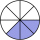 What is ⅔ × ⅚?
What is ⅔ × ⅚? - Calculated 7916
 The raw wood beam weighs 85 kg. It is calculated that drying will reduce its weight in a ratio of 5: 6. What will be its weight after drying?
The raw wood beam weighs 85 kg. It is calculated that drying will reduce its weight in a ratio of 5: 6. What will be its weight after drying? - Word MATEMATIKA
 How many words can be created from the phrase MATEMATIKA by changing the letters' order, regardless of whether the words are meaningful?
How many words can be created from the phrase MATEMATIKA by changing the letters' order, regardless of whether the words are meaningful? - Triangle 42
 Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=?
Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=? - Cocoa
 3/4 cup of cocoa is needed to make a chocolate bar. If Rohan wants to make 16 chocolate bars, how many cups of cocoa are required?
3/4 cup of cocoa is needed to make a chocolate bar. If Rohan wants to make 16 chocolate bars, how many cups of cocoa are required? - Triangle 35881
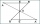 The sum of the lengths of the two sides b + c = 12 cm Beta angle = 68 Gamma angle = 42 draw triangle ABC
The sum of the lengths of the two sides b + c = 12 cm Beta angle = 68 Gamma angle = 42 draw triangle ABC - Beth wants
 Beth wants to give 1/4 pizza to each of her 6 friends. Which choice does not show the number of pizzas Beth needs?
Beth wants to give 1/4 pizza to each of her 6 friends. Which choice does not show the number of pizzas Beth needs? - Finite arithmetic sequence
 How many numbers should be inserted between the numbers 1 and 25 so that all numbers create a finite arithmetic sequence and that the sum of all members of this group is 117?
How many numbers should be inserted between the numbers 1 and 25 so that all numbers create a finite arithmetic sequence and that the sum of all members of this group is 117? - Suspended 82617
 A round steel weight (ρ1=7800 kg/m3) is suspended on a thread and immersed in water (ρ2=1000 kg/m3). The volume of the weight is 1dm³. With what force is the thread stretched?
A round steel weight (ρ1=7800 kg/m3) is suspended on a thread and immersed in water (ρ2=1000 kg/m3). The volume of the weight is 1dm³. With what force is the thread stretched? - Diameter 24181
 What is the weight of a lead ball with a diameter of 3 cm if the density of lead is 11340 kg/m cubic?
What is the weight of a lead ball with a diameter of 3 cm if the density of lead is 11340 kg/m cubic? - Dina was
 Dina was paid P8.30 per hour and a time-and-a-half for all hours worked in excess of 40 hours per week. She worked 12 hours on Monday, 6 1/2 on Tuesday, 9 on Wednesday,8 on Thursday, and 10 1/2 on Friday. What was her total pay for the week?
Dina was paid P8.30 per hour and a time-and-a-half for all hours worked in excess of 40 hours per week. She worked 12 hours on Monday, 6 1/2 on Tuesday, 9 on Wednesday,8 on Thursday, and 10 1/2 on Friday. What was her total pay for the week?
more math problems »
