Length + triangle - practice problems - page 6 of 41
Number of problems found: 803
- A construction
 A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find
A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find - Maggie
 Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree.
Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree. - Perpendicular 73574
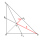 The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line.
The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line. - Triangle 73464
 The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much.
The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much.
- Kilometers 73344
 How many meters will the track ascend if it is 200 kilometers long and the ascent is 7 per mille?
How many meters will the track ascend if it is 200 kilometers long and the ascent is 7 per mille? - Binibini
 Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths)
Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths) - Perpendicular 73264
 The perimeter of a right triangle is equal to 30 centimeters. Calculate the perpendicular b if a = 5 centimeters and c = 13 centimeters. A natural number expresses the length of the perpendicular b.
The perimeter of a right triangle is equal to 30 centimeters. Calculate the perpendicular b if a = 5 centimeters and c = 13 centimeters. A natural number expresses the length of the perpendicular b. - A flagpole
 A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string?
A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string? - Calculate 73024
 Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
- A chord
 In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the cord at the center of the circle Hence find the length of the minor arc cut off by the chord.
In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the cord at the center of the circle Hence find the length of the minor arc cut off by the chord. - A man 7
 A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles in the direction of N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.)
A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles in the direction of N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.) - A rhombus 4
 A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution. - Fencing material
 Ailey bought 10 meters of wire fencing material to enclose her triangular flower garden. If the lengths of the sides of the triangular garden are 2 ½ meters, 3 ⅔ meters, 2 ⅙ meters, how long will the excess wire fencing material be?
Ailey bought 10 meters of wire fencing material to enclose her triangular flower garden. If the lengths of the sides of the triangular garden are 2 ½ meters, 3 ⅔ meters, 2 ⅙ meters, how long will the excess wire fencing material be? - Observatory 71934
 The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee
The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee
- Designated 71874
 The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started.
The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started. - The airplane
 The airplane sights a runway at an angle of depression of 23°. It is flying at an altitude of 3 kilometers above the ground. What is the horizontal distance of the airplane from the airport?
The airplane sights a runway at an angle of depression of 23°. It is flying at an altitude of 3 kilometers above the ground. What is the horizontal distance of the airplane from the airport? - An angle of depression
 The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse?
The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse? - Triangle 71404
 Which three lines of a given length can be three sides of a triangle? A / 42mm; 22mm; 12mm; B / 5cm, 50mm, 6cm; C / 10m, 5m, 50dm; D / 2.1cm, 4.2cm, 1.9cm
Which three lines of a given length can be three sides of a triangle? A / 42mm; 22mm; 12mm; B / 5cm, 50mm, 6cm; C / 10m, 5m, 50dm; D / 2.1cm, 4.2cm, 1.9cm - Circumference 71304
 The PQR triangle with a circumference of 25.5 cm has sides in a ratio of 4:6:5. Determine the lengths of its sides.
The PQR triangle with a circumference of 25.5 cm has sides in a ratio of 4:6:5. Determine the lengths of its sides.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
