Length + angle - practice problems
Number of problems found: 305
- An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - A lighthouse
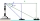 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - A random
 A random sample of 225 nails in a manufacturing company is gathered. The engineer specified that the specified length of a nail must be 8 cm having a standard deviation of 0.04 cm. It shows from the sample that the average length of the nails is 8.055 cm.
A random sample of 225 nails in a manufacturing company is gathered. The engineer specified that the specified length of a nail must be 8 cm having a standard deviation of 0.04 cm. It shows from the sample that the average length of the nails is 8.055 cm. - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - Isosceles 83247
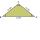 Calculate the lengths of the sides in an isosceles triangle, given the height (to the base) Vc= 8.8cm and the angle at the base alpha= 38°40`.
Calculate the lengths of the sides in an isosceles triangle, given the height (to the base) Vc= 8.8cm and the angle at the base alpha= 38°40`. - Construction 83208
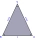 An isosceles triangle ABY with a base AB of length 5 cm and an angle at the main vertex of 50°. Write down the construction progress.
An isosceles triangle ABY with a base AB of length 5 cm and an angle at the main vertex of 50°. Write down the construction progress. - Calculate 83160
 Calculate the distance of point A[ 4; 2; -3 ] from the plane : 2x - 2y + z + 5 = 0
Calculate the distance of point A[ 4; 2; -3 ] from the plane : 2x - 2y + z + 5 = 0 - Parallelogram 82695
 Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals.
Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals. - Calculate 82578
 The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A.
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Hypotenuse 82370
 A line segment AA1 of length 6 cm is given. Construct all triangles ABC for which AA1 is the hypotenuse, side length BC is 5 cm, and angle gamma is 60°.
A line segment AA1 of length 6 cm is given. Construct all triangles ABC for which AA1 is the hypotenuse, side length BC is 5 cm, and angle gamma is 60°. - Hypotenuse 82331
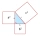 Given a right triangle KLM with a right angle at M. What is the magnitude of the hypotenuse m if the magnitude of the normal to the hypotenuse m is 4?
Given a right triangle KLM with a right angle at M. What is the magnitude of the hypotenuse m if the magnitude of the normal to the hypotenuse m is 4? - Length 82244
 What path will the tip of the minute hand of length 5 dm cover on the clock in 2 hours?
What path will the tip of the minute hand of length 5 dm cover on the clock in 2 hours? - Vertically 82162
 The pole is stuck vertically into the ground. The protruding length is 1m. What is the length of the shadow cast when the sun is just 50° above the horizon?
The pole is stuck vertically into the ground. The protruding length is 1m. What is the length of the shadow cast when the sun is just 50° above the horizon? - Determine 82032
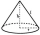 Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base. - Difference 81888
 The ropeway climbs at an angle of 22°30'. Calculate its length if the height difference between the lower and upper station is 560m. Sketch a picture
The ropeway climbs at an angle of 22°30'. Calculate its length if the height difference between the lower and upper station is 560m. Sketch a picture - Circumference 81778
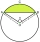 Points A and B lie on the circle k. The circumference of the circle k is 40 CM, and the length of the circular arc AB is 10 CM. Determine the size of the angle ABS.
Points A and B lie on the circle k. The circumference of the circle k is 40 CM, and the length of the circular arc AB is 10 CM. Determine the size of the angle ABS. - Shortest 81627
 What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole?
What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole? - Calculate 81590
 Calculate the central angle if r = 72 cm and the arc length is 12.4 cm.
Calculate the central angle if r = 72 cm and the arc length is 12.4 cm. - Archaeologists 81478
 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
