Line + reason - practice problems
Number of problems found: 54
- Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Probability 81637
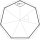 We randomly select three different points from the vertices of a regular heptagon and connect them with line segments. The probability that the resulting triangle will be isosceles is equal to: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7
We randomly select three different points from the vertices of a regular heptagon and connect them with line segments. The probability that the resulting triangle will be isosceles is equal to: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7 - Quadrilateral calc
 The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc
The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc - Distances 79974
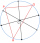 The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be
The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be - Equilateral 75284
 Given are 6 line segments with lengths of 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm. How many equilateral triangles can make from them? List all the options.
Given are 6 line segments with lengths of 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm. How many equilateral triangles can make from them? List all the options. - Calculate 73024
 Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m. - Probability 59073
 A group of n people, including Jano and Fero, randomly line up. What probability will there be exactly r people (r
A group of n people, including Jano and Fero, randomly line up. What probability will there be exactly r people (r - Construction 55311
 Construct a KLM triangle where side k is 6.7 cm, the line to the k side is 4.1 cm, and the LKM angle is 63 degrees. Write the construction procedure.
Construct a KLM triangle where side k is 6.7 cm, the line to the k side is 4.1 cm, and the LKM angle is 63 degrees. Write the construction procedure. - Intersections 49433
 Draw a graph of the function given by the equation y = -2x +3, determine its intersections with the coordinate axes, and complete the missing coordinates A [3;? ], B [?; 8].
Draw a graph of the function given by the equation y = -2x +3, determine its intersections with the coordinate axes, and complete the missing coordinates A [3;? ], B [?; 8]. - Divide an isosceles triangle
 How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)? - Double-track line
 A 160 m long passenger train runs on a double-track line in one direction at a constant speed of 54 km/h, and a 240 m long express train in the opposite direction. a) How fast is the express train if passing the passenger train driver for 6 s? b) How long
A 160 m long passenger train runs on a double-track line in one direction at a constant speed of 54 km/h, and a 240 m long express train in the opposite direction. a) How fast is the express train if passing the passenger train driver for 6 s? b) How long - Points in space
 There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points?
There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points? - Intersections 26781
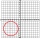 A rectangular grid consists of two mutually perpendicular systems of parallel lines with a distance of 2. We throw a circle with a diameter of 1 on this plane. Calculate the probability that this circle: a) overlaps one of the straight lines; b) do any of
A rectangular grid consists of two mutually perpendicular systems of parallel lines with a distance of 2. We throw a circle with a diameter of 1 on this plane. Calculate the probability that this circle: a) overlaps one of the straight lines; b) do any of - Dodecagon
 Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees.
Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees. - Identical 20963
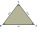 In which triangles is the line identical with the height?
In which triangles is the line identical with the height? - Determined 16233
 How many lines are determined by 5 points if three lie in one line?
How many lines are determined by 5 points if three lie in one line? - Three parallels
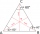 The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle. - Three lines
 At 6 AM, three bus lines depart from the station. The first line has an interval of 24 minutes. The second line has an interval of 15 minutes. The third line runs at regular intervals of more than 1 minute. The third line runs at the same time as the firs
At 6 AM, three bus lines depart from the station. The first line has an interval of 24 minutes. The second line has an interval of 15 minutes. The third line runs at regular intervals of more than 1 minute. The third line runs at the same time as the firs - Construct 10921
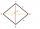 Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all options
Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all options - Different 9711
 A new bus route network was built. There are three stops on each line. In addition, every two lines either do not have a common stop or have only one common stop. What is the largest number of tracks there can be in a town if we know there are only nine d
A new bus route network was built. There are three stops on each line. In addition, every two lines either do not have a common stop or have only one common stop. What is the largest number of tracks there can be in a town if we know there are only nine d
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
