Line + quadratic equation - practice problems
Number of problems found: 28
- Determine 83003
 Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common.
Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common. - Parametrically 82990
 Calculate the sum of the x-coordinates of the intersections of the circle given by the equation (x - 1)²+ y² = 1 and the line given parametrically x = t, y = t , where t∈R.
Calculate the sum of the x-coordinates of the intersections of the circle given by the equation (x - 1)²+ y² = 1 and the line given parametrically x = t, y = t , where t∈R. - Coordinate 82855
 What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system?
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system? - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
- Determine 82478
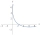 Determine the equation of the parabola that has the point F = [3,2] as its focus and the line x+y+1=0 as its shift line.
Determine the equation of the parabola that has the point F = [3,2] as its focus and the line x+y+1=0 as its shift line. - Determine 82394
 Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t,
Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t, - Intersection of Q2 with line
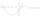 The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the
The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the - Magnitudes 64704
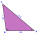 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - The tangent line
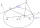 Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1.
Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1.
- Tangents to ellipse
 Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1].
Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1]. - Isosceles triangle
 In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Points in space
 There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points?
There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points? - On a line
 On a line p : 3 x - 4 y - 3 = 0, determine the point C equidistant from points A[4, 4] and B[7, 1].
On a line p : 3 x - 4 y - 3 = 0, determine the point C equidistant from points A[4, 4] and B[7, 1]. - Suppose
 Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not?
Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not?
- Three parallels
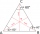 The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle. - Eq2 2
 Solve the following equation with quadratic members and rational function: (x²+1)/(x-4) + (x²-1)/(x+3) = 23
Solve the following equation with quadratic members and rational function: (x²+1)/(x-4) + (x²-1)/(x+3) = 23 - On line
 On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0].
On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0]. - Distance problem
 A=(x, x) B=(1,4) Distance AB=√5, find x;
A=(x, x) B=(1,4) Distance AB=√5, find x; - Right triangle from axes
 A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment?
A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
