Natural numbers + modulo - practice problems
Number of problems found: 10
- A labourer
A laborer who works five days a week starts at 10 AM on Monday. If he works for 56 days, on which day will he complete the job? - Remainders
It is given a set of numbers { 117; 136; 363; 419; 575; 651 }. Divide these numbers by number 58 and determine a set of remainders. As a result, write the sum of these remainders. - Divisibility
Is the number 728267 exactly divisible by 8? (the result is the integer, and/or remainder is zero) - Organizes 4152
Shepherd has less than 500 sheep. If he organizes them in 4 rows, he will remain three sheep. If he manages them in 5 rows, he will remain four sheep. If he arranges them in 6 rows, he will remain five sheep. But it can manage them exactly in 7 rows. How
- Fraction to decimal infinite
Find which digit is at 1000th place after the decimal point in the decimal expansion of the fraction 9/28. - Modulo
Find x in the modulo equation: 47x = 4 (mod 9) Hint - read as what number 47x divided by 9 (modulo 9) gives remainder 4. - Big number What is the remainder when dividing 10 by 9 to 47 - 111?
- Restriction 7442
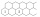The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top - Twos
Vojta started writing the number this year, 2019202020192020, into the workbook. And so he kept going. When he wrote 2020 digits, he no longer enjoyed it. How many twos did he write?
The natural number n has at least 73 two-digit divisors. Prove that one of them is the number 60. Also, give an example of the number n, which has exactly 73 double-digit divisors, including a proper justification.We apologize, but in this category are not a lot of examples.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
