Planimetrics - practice problems - page 8 of 169
Study plane measurements, including angles, distances, and areas. In other words - measurement and calculation of shapes in the plane. Perimeter and area of plane shapes.Number of problems found: 3380
- X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
- Using 4
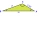 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - Trigonometric fx
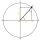 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Calculate 83265
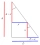 Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm.
Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm. - Calculate 83203
 Calculate the area of a circle whose radius is 9m. (in square meters)
Calculate the area of a circle whose radius is 9m. (in square meters) - Direction 83124
 The mining tower's wheel has a diameter of 150 cm. If the wheel turns in the same direction seventy times, how many m will the elevator cage descend?
The mining tower's wheel has a diameter of 150 cm. If the wheel turns in the same direction seventy times, how many m will the elevator cage descend?
- Measures 82530
 How many meters of mesh are needed to fence a square plot whose side measures 20m?
How many meters of mesh are needed to fence a square plot whose side measures 20m? - Triangular 82269
 A gardener plants one row of tulips around a triangular bed with sides of 5 m, 6 m, and 10 m. How many tulip bulbs does he need if he wants to plant 8 bulbs on a length of 1 m?
A gardener plants one row of tulips around a triangular bed with sides of 5 m, 6 m, and 10 m. How many tulip bulbs does he need if he wants to plant 8 bulbs on a length of 1 m? - Length 82244
 What path will the tip of the minute hand of length 5 dm cover on the clock in 2 hours?
What path will the tip of the minute hand of length 5 dm cover on the clock in 2 hours? - Square-shaped 82159
 The square-shaped garden has a hedge on three sides. Its length is 36 meters. What is the content of the garden in m²?
The square-shaped garden has a hedge on three sides. Its length is 36 meters. What is the content of the garden in m²? - Dimensions 82000
 How much will we pay for laying a wooden floor in the living room of an apartment with dimensions of 40dm and 50dm if 1 square meter of wooden floor costs 12.4 euros?
How much will we pay for laying a wooden floor in the living room of an apartment with dimensions of 40dm and 50dm if 1 square meter of wooden floor costs 12.4 euros?
- Tablecloth 81847
 A square tablecloth measures 80 cm so that it protrudes 33 cm on the sides; calculate how big it is.
A square tablecloth measures 80 cm so that it protrudes 33 cm on the sides; calculate how big it is. - Rectangular 81838
 The rectangular pool has dimensions of 12m and 25m. They built a 2-wide sidewalk around the pool and a fence around the sidewalk. How long is the fence if they leave 1 m for the entrance hole?
The rectangular pool has dimensions of 12m and 25m. They built a 2-wide sidewalk around the pool and a fence around the sidewalk. How long is the fence if they leave 1 m for the entrance hole? - Circumference 81778
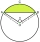 Points A and B lie on the circle k. The circumference of the circle k is 40 CM, and the length of the circular arc AB is 10 CM. Determine the size of the angle ABS.
Points A and B lie on the circle k. The circumference of the circle k is 40 CM, and the length of the circular arc AB is 10 CM. Determine the size of the angle ABS. - Half-circles 81731
 A skier skis down a black slope. He makes a total of 31 half-circles while going down the hill. The radius of one semicircle is 4m. What distance did he travel?
A skier skis down a black slope. He makes a total of 31 half-circles while going down the hill. The radius of one semicircle is 4m. What distance did he travel? - Calculate 81590
 Calculate the central angle if r = 72 cm and the arc length is 12.4 cm.
Calculate the central angle if r = 72 cm and the arc length is 12.4 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
