Polygon + angle - practice problems
Number of problems found: 133
- The number 10
 The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon. - One side 4
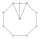 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - The interior
 The interior angle of a regular polygon is x. If x is 9° less than the average of 153° and 145°, find the number of sides of the polygon.
The interior angle of a regular polygon is x. If x is 9° less than the average of 153° and 145°, find the number of sides of the polygon. - n-gon
 Gabo draws n-gon, which angles are consecutive members of an arithmetic sequence. The smallest angle is 70° biggest 170°. How many sides have Gabo's n-gon?
Gabo draws n-gon, which angles are consecutive members of an arithmetic sequence. The smallest angle is 70° biggest 170°. How many sides have Gabo's n-gon? - Each with each
 Five pupils from 3A class played table tennis. How many matches did they play with each other?
Five pupils from 3A class played table tennis. How many matches did they play with each other? - Interior angles - sum
 For the sum s of the interior angles of a polygon, where n is the number of its sides, the relation s=(n−2)⋅180 degrees applies. How many sides does a polygon have if the sum of its interior angles is 900°?
For the sum s of the interior angles of a polygon, where n is the number of its sides, the relation s=(n−2)⋅180 degrees applies. How many sides does a polygon have if the sum of its interior angles is 900°? - Regular n-gon
 In a regular n-angle polygon, the internal angle is 144 degrees. Find the number n indicating the number of sides of this polygon.
In a regular n-angle polygon, the internal angle is 144 degrees. Find the number n indicating the number of sides of this polygon. - Sum of inner angles
 Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees.
Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees. - Angles of a hexagon
 Find the interior angles of a hexagon if the sizes of the angles form an arithmetic sequence, and the smallest angle is 70°.
Find the interior angles of a hexagon if the sizes of the angles form an arithmetic sequence, and the smallest angle is 70°. - Polygon 42
 Which polygon has 42 more diagonals than sides?
Which polygon has 42 more diagonals than sides? - 9-gon
 The sum of interior angles of 9-gon is:
The sum of interior angles of 9-gon is: - Diagonals
 What x-gon has 54 diagonals?
What x-gon has 54 diagonals? - N-gon
 How many diagonals have convex 30-gon?
How many diagonals have convex 30-gon? - Candy - MO
 Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t
Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t - Inner angles
 The inner angles of the triangle are 30°, 45°, and 105° and its longest side is 10 cm. Calculate the shortest side length, and write the result in cm up to two decimal places.
The inner angles of the triangle are 30°, 45°, and 105° and its longest side is 10 cm. Calculate the shortest side length, and write the result in cm up to two decimal places. - Similarity n-gon
 9-gones ABCDEFGHI and A'B'C'D'E'F'G'H'I' are similar. The area of 9-gon ABCDEFGHI is S1=190 dm², and the diagonal length GD is 32 dm. Calculate the area of the 9-gon A'B'C'D'E'F'G'H'I' if G'D' = 13 dm.
9-gones ABCDEFGHI and A'B'C'D'E'F'G'H'I' are similar. The area of 9-gon ABCDEFGHI is S1=190 dm², and the diagonal length GD is 32 dm. Calculate the area of the 9-gon A'B'C'D'E'F'G'H'I' if G'D' = 13 dm. - Center of gravity
 In the isosceles triangle ABC is the ratio of the lengths of AB and the height to AB 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT.
In the isosceles triangle ABC is the ratio of the lengths of AB and the height to AB 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT. - Complementary 81152
 In a certain polygon, the ratio of the sum of the sizes of its internal angles and the sum of the sizes of the complementary angles is 2:5. How many vertices does this polygon have?
In a certain polygon, the ratio of the sum of the sizes of its internal angles and the sum of the sizes of the complementary angles is 2:5. How many vertices does this polygon have? - Regular polygons
 Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x?
Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
