Polygon + surface area - practice problems
Number of problems found: 43
- Pentagonal pyramid
 Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm. - Calculate
 Calculate the surface of a regular eleven-sided prism; if the area of its base is 58 cm2, the edge of the base is 6cm long, and the height of the prism is 21 cm.
Calculate the surface of a regular eleven-sided prism; if the area of its base is 58 cm2, the edge of the base is 6cm long, and the height of the prism is 21 cm. - A dodecagon
 Find the surface area of a regular 12-sided polygon if its side is a = 12 cm.
Find the surface area of a regular 12-sided polygon if its side is a = 12 cm. - Six-sided 44151
 The parasol has the shape of the shell of a regular six-sided pyramid, whose base edge is a=6dm and height v=25cm. How much fabric is needed to make a parasol if we count 10% for joints and waste?
The parasol has the shape of the shell of a regular six-sided pyramid, whose base edge is a=6dm and height v=25cm. How much fabric is needed to make a parasol if we count 10% for joints and waste? - Octahedron - sum
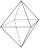 On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al
On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Pentagonal pyramid
 The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid.
The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid. - Calculate 6178
 Calculate the plastic area of a 5-sided prism if the surface of the prism is 258 cm2, and one base has an area of 64.6 cm². Enter the result in the form of the decimal number in cm².
Calculate the plastic area of a 5-sided prism if the surface of the prism is 258 cm2, and one base has an area of 64.6 cm². Enter the result in the form of the decimal number in cm². - Calculate 31651
 Calculate the surface of a regular 5-sided prism with a base area of 60 dm² if the length of the edge of the lower base is four dm. The height of the prism is 1.3 m.
Calculate the surface of a regular 5-sided prism with a base area of 60 dm² if the length of the edge of the lower base is four dm. The height of the prism is 1.3 m. - Hexagonal 29141
 Calculate the volume and surface of a regular hexagonal prism with a base edge a = 30 m and a side edge b = 50 m.
Calculate the volume and surface of a regular hexagonal prism with a base edge a = 30 m and a side edge b = 50 m. - Hexagonal prism
 Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm.
Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm. - Hexaprism container
 Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm.
Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm. - Hexagonal pyramid
 Calculate a regular hexagonal pyramid's volume and surface area with a base edge a = 30 m and a side edge b = 50 m.
Calculate a regular hexagonal pyramid's volume and surface area with a base edge a = 30 m and a side edge b = 50 m. - Tetrahedron 46451
 Calculate the surface of a regular tetrahedron if the length of the wall height v = 1 dm.
Calculate the surface of a regular tetrahedron if the length of the wall height v = 1 dm. - Top of the tower
 The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join - Octagonal tank
 The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness.
The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness. - 9-gon pyramid
 Calculate a nine-sided pyramid's volume and surface, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm.
Calculate a nine-sided pyramid's volume and surface, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm. - Nine-sided 36071
 Calculate the surface area and volume of a regular nine-sided pyramid if the radius of the circle inscribed in the base measures ρ = 12 cm and the height of the pyramid is 24 cm
Calculate the surface area and volume of a regular nine-sided pyramid if the radius of the circle inscribed in the base measures ρ = 12 cm and the height of the pyramid is 24 cm - Decimeters 2551
 The cardboard packaging without a lid has the shape of a regular hexagonal prism with a main edge that is 12 cm long and 15 cm high. How much cardboard is used to make five packages if 10% of the cardboard is added for folds? Give results in square decime
The cardboard packaging without a lid has the shape of a regular hexagonal prism with a main edge that is 12 cm long and 15 cm high. How much cardboard is used to make five packages if 10% of the cardboard is added for folds? Give results in square decime - Hexagonal prism
 The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism. - Hexagonal 3468
 The box of a regular hexagonal prism is 4 cm high, and the lid has sides 20 cm long. How much cardboard is needed to make it? (No part is double)
The box of a regular hexagonal prism is 4 cm high, and the lid has sides 20 cm long. How much cardboard is needed to make it? (No part is double)
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
