Prism + Pythagorean theorem - practice problems
Number of problems found: 99
- Centimeters 6596
 The jewelry box is in the shape of a four-sided prism with the base of an isosceles trapezoid with sides a=15 centimeters, b is equal to 9 centimeters, c is equal to 10 centimeters, c is equal to 7 whole 4 centimeters. How much fabric is needed to cover a
The jewelry box is in the shape of a four-sided prism with the base of an isosceles trapezoid with sides a=15 centimeters, b is equal to 9 centimeters, c is equal to 10 centimeters, c is equal to 7 whole 4 centimeters. How much fabric is needed to cover a - Triangular prism
 The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism.
The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism. - Octagonal tank
 The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness.
The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness. - Four sided prism
 Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane.
Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane. - Quadrilateral 24161
 Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated?
Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated? - Wooden prism
 Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³.
Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³. - Base of prism
 The base of the perpendicular prism is a rectangular triangle whose legs lengths are at a 3:4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm².
The base of the perpendicular prism is a rectangular triangle whose legs lengths are at a 3:4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm². - Whitewashed 3483
 The pool is in the shape of a vertical prism with a bottom in the shape of an isosceles trapezoid with dimensions of the bases of the trapezoid 10m and 18m, and arms 7m are 2m deep. During spring cleaning, the bottom and walls of the pool must be whitewas
The pool is in the shape of a vertical prism with a bottom in the shape of an isosceles trapezoid with dimensions of the bases of the trapezoid 10m and 18m, and arms 7m are 2m deep. During spring cleaning, the bottom and walls of the pool must be whitewas - Triangular prism
 The triangular prism has a base in the shape of a right triangle, the legs of which are 9 cm and 40 cm long. The height of the prism is 20 cm. What is its volume cm³? And the surface cm²?
The triangular prism has a base in the shape of a right triangle, the legs of which are 9 cm and 40 cm long. The height of the prism is 20 cm. What is its volume cm³? And the surface cm²? - Rhombus base
 Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 12 cm and u2 = 15 cm. Prism height is twice the base edge length.
Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 12 cm and u2 = 15 cm. Prism height is twice the base edge length. - Dimensions 6578
 How many m² of fabric is needed to make a tent of a regular 3-sided prism if it is necessary to count on a 2% reserve of fabric? Dimensions - 2m 1.6m and height 1.4m
How many m² of fabric is needed to make a tent of a regular 3-sided prism if it is necessary to count on a 2% reserve of fabric? Dimensions - 2m 1.6m and height 1.4m - Quadrilateral prism
 The height of a regular quadrilateral prism is v = 10 cm, and the deviation of the body diagonal from the base is 60°. Determine the length of the base edges, the surface, and the prism's volume.
The height of a regular quadrilateral prism is v = 10 cm, and the deviation of the body diagonal from the base is 60°. Determine the length of the base edges, the surface, and the prism's volume. - Support colum
 Calculate the support column's volume and surface, which is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. Column height is 1. 5m.
Calculate the support column's volume and surface, which is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. Column height is 1. 5m. - Tent
 Calculate how many liters of air will fit in the tent with a shield in the shape of an isosceles right triangle with legs r = 3 m long, the height = 1.5 m, and a side length d = 5 m.
Calculate how many liters of air will fit in the tent with a shield in the shape of an isosceles right triangle with legs r = 3 m long, the height = 1.5 m, and a side length d = 5 m. - Right-angled 6034
 A three-sided prism has a base in the shape of a right-angled triangle with a length of 5 cm. The giant wall of the prism shell has a volume of 104 cm². The prism is 8 cm high. Calculate the volume and surface area of the prism.
A three-sided prism has a base in the shape of a right-angled triangle with a length of 5 cm. The giant wall of the prism shell has a volume of 104 cm². The prism is 8 cm high. Calculate the volume and surface area of the prism. - Perpendicular prism network
 Find the volume and surface of a triangular prism with the base of a right triangle, the network of which is 4 cm 3 cm (perpendiculars) and nine centimeters (height of the prism).
Find the volume and surface of a triangular prism with the base of a right triangle, the network of which is 4 cm 3 cm (perpendiculars) and nine centimeters (height of the prism). - Hexagonal prism
 The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism. - Quadrilateral 47493
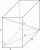 A regular quadrilateral prism ABCDEFGH has a base edge A B 8 cm long and 6 cm high. Point M is the center of the edge AE. Determine the distance of point M from the BDH plane.
A regular quadrilateral prism ABCDEFGH has a base edge A B 8 cm long and 6 cm high. Point M is the center of the edge AE. Determine the distance of point M from the BDH plane. - Prism - right isosceles
 Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm.
Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm. - Isosceles + prism
 Calculate the volume of the perpendicular prism if its height is 17.5 cm and the base is an isosceles triangle with a base length of 5.8 cm and an arm's length of 3.7 cm
Calculate the volume of the perpendicular prism if its height is 17.5 cm and the base is an isosceles triangle with a base length of 5.8 cm and an arm's length of 3.7 cm
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
