Pythagorean theorem + real numbers - practice problems
Number of problems found: 24
- Rectangle SS
 The perimeter of a rectangle is 268 cm, and its diagonal is 99.3 cm. Determine the dimensions of the rectangle.
The perimeter of a rectangle is 268 cm, and its diagonal is 99.3 cm. Determine the dimensions of the rectangle. - Rhombus ABCD
 Rhombus ABCD, |AC| = 63 cm, |BD| = 50 cm. Calculate the perimeter of the rhombus ABCD.
Rhombus ABCD, |AC| = 63 cm, |BD| = 50 cm. Calculate the perimeter of the rhombus ABCD. - Diagonals of the rhombus
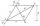 Calculate the height of the rhombus whose diagonals are 18 cm and 6 cm.
Calculate the height of the rhombus whose diagonals are 18 cm and 6 cm. - Medians
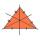 Calculate the sides of a right triangle if the length of the medians to the legs are ta = 25 cm and tb=30 cm.
Calculate the sides of a right triangle if the length of the medians to the legs are ta = 25 cm and tb=30 cm.
- Square 2
 Points D[10,-8] and B[4,5] are opposed vertices of the square ABCD. Calculate the area of the square ABCD.
Points D[10,-8] and B[4,5] are opposed vertices of the square ABCD. Calculate the area of the square ABCD. - Area 4gon
 Calculate the area of 4-gon, two, and the two sides are equal and parallel with lengths 11, 5, 11, and 5. Inner angles are 45°, 135°,45°, 135°.
Calculate the area of 4-gon, two, and the two sides are equal and parallel with lengths 11, 5, 11, and 5. Inner angles are 45°, 135°,45°, 135°. - Sea
 How far can you see from the ship's mast, whose peak is at 14 meters above sea level? (Earth's radius is 6370 km).
How far can you see from the ship's mast, whose peak is at 14 meters above sea level? (Earth's radius is 6370 km). - Trigonometric functions
 In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20)
In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20) - Right Δ
 A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle.
A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle.
- Garden
 The square garden area is 2/9 of triangle garden with sides 160 m, 100 m, and 100 m. How many meters of fencing need to fence a square garden?
The square garden area is 2/9 of triangle garden with sides 160 m, 100 m, and 100 m. How many meters of fencing need to fence a square garden? - Rectangle
 The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle.
The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle. - ABS, ARG, CONJ, RECIPROCAL
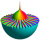 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - Movement
 From the crossing of two perpendicular roads started two cyclists (each on a different road). One runs at an average speed of 28 km/h, and the second 24 km/h. Determine the distance between them after 45 minutes of cycling.
From the crossing of two perpendicular roads started two cyclists (each on a different road). One runs at an average speed of 28 km/h, and the second 24 km/h. Determine the distance between them after 45 minutes of cycling. - Short cut
 Imagine that you are going to a friend. That path has a length 120 meters. Then turn doprava and go other 630 meters, and you are at a friend's. The question is, how much will the journey be shorter if you go direct across the field?
Imagine that you are going to a friend. That path has a length 120 meters. Then turn doprava and go other 630 meters, and you are at a friend's. The question is, how much will the journey be shorter if you go direct across the field?
- Gimli Glider
 Aircraft Boeing 767 lose both engines at 42000 feet. The plane captain maintains optimum gliding conditions. Every minute, lose 1910 feet and maintain constant speed 211 knots. Calculate how long it takes for a plane to hit the ground from engine failure.
Aircraft Boeing 767 lose both engines at 42000 feet. The plane captain maintains optimum gliding conditions. Every minute, lose 1910 feet and maintain constant speed 211 knots. Calculate how long it takes for a plane to hit the ground from engine failure. - Square
 Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD.
Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD. - Circle
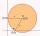 Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r²
Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r² - Cubes
 One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm².
One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm². - Cone A2V
 The cone's surface in the plane is a circular arc with a central angle of 126° and area 415 cm². Calculate the volume of a cone.
The cone's surface in the plane is a circular arc with a central angle of 126° and area 415 cm². Calculate the volume of a cone.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
