Pythagorean theorem + circle - practice problems - page 7 of 12
Number of problems found: 226
- MO circles
 Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th
Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th - Infinity
 A square with a side 19 long is an inscribed circle, and the circle is inscribed next square, circle, and so on to infinity. Calculate the sum of the area of all these squares.
A square with a side 19 long is an inscribed circle, and the circle is inscribed next square, circle, and so on to infinity. Calculate the sum of the area of all these squares. - Hypotenuses 83154
 In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle. - Perpendicular 70824
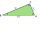 One perpendicular to the ABC right triangle has a length a = 14 cm, and a radius of the circle inscribed in this triangle r = 5 cm. Find the size of the diaphragm and its second perpendicular.
One perpendicular to the ABC right triangle has a length a = 14 cm, and a radius of the circle inscribed in this triangle r = 5 cm. Find the size of the diaphragm and its second perpendicular.
- Rectangle
 The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle.
The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle. - Quatrefoil 81138
 Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters.
Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters. - Overload
 Calculate how many g's (gravity accelerations) the glider pilot when turning the horizontal circles of radius 148 m flying at 95 km/h. Centripetal acceleration is proportional to the square of the speed and inversely proportional to the radius of rotation
Calculate how many g's (gravity accelerations) the glider pilot when turning the horizontal circles of radius 148 m flying at 95 km/h. Centripetal acceleration is proportional to the square of the speed and inversely proportional to the radius of rotation - Situation 70644
 How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - ABS, ARG, CONJ, RECIPROCAL
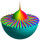 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
- Radio radius
 Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both
Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both - Eq triangle minus arcs
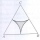 In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cu
In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cu - A bridge
 The bridge over the river has the shape of an arc. The bridge is 10 feet above the water at the center of the river. At 27 feet from the river's edge, the bridge is 9 feet above the water. How wide is the river?
The bridge over the river has the shape of an arc. The bridge is 10 feet above the water at the center of the river. At 27 feet from the river's edge, the bridge is 9 feet above the water. How wide is the river? - Metal washers
 Metal washers with a diameter of 80 mm are cut from a strip of steel sheet with a width of 10 cm and a length of 2 m. When two adjacent circles meet, calculate the material waste percentage if no material is lost.
Metal washers with a diameter of 80 mm are cut from a strip of steel sheet with a width of 10 cm and a length of 2 m. When two adjacent circles meet, calculate the material waste percentage if no material is lost. - Archaeologists 81478
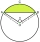 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
- Circumscribed 6568
 In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - Tangent 3
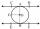 In a circle with a center O radius is 4√5 cm. EC is the tangent to the circle at point D. Segment AB is a given circle's DIAMETER. POINT A is joined with POINT E, and POINT B is joined with POINT C. Find DC if BC IS 8cm.
In a circle with a center O radius is 4√5 cm. EC is the tangent to the circle at point D. Segment AB is a given circle's DIAMETER. POINT A is joined with POINT E, and POINT B is joined with POINT C. Find DC if BC IS 8cm. - Intersect 6042
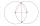 Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles?
Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles? - Circumscribed 5465
 Inside the rectangle ABCD, the points E and F lie so that the line segments EA, ED, EF, FB, and FC are congruent. Side AB is 22 cm long, and the circle circumscribed by triangle AFD has a radius of 10 cm. Determine the length of side BC.
Inside the rectangle ABCD, the points E and F lie so that the line segments EA, ED, EF, FB, and FC are congruent. Side AB is 22 cm long, and the circle circumscribed by triangle AFD has a radius of 10 cm. Determine the length of side BC. - Nonagon
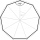 Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
