Pythagorean theorem + percentages - practice problems
Number of problems found: 83
- Using 4
 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - General right triangle
 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - Isosceles triangle
 Find the area of an isosceles triangle whose leg is twice the base, b=1
Find the area of an isosceles triangle whose leg is twice the base, b=1 - Equilateral triangle
 Calculate the side of an equilateral triangle if its area is 886 mm².
Calculate the side of an equilateral triangle if its area is 886 mm². - Waste
 How many percents are waste from a circular plate with a radius of 1 m from which we cut a square with the highest area?
How many percents are waste from a circular plate with a radius of 1 m from which we cut a square with the highest area? - Calculate square 2556
 Calculate the arm length b of the trapezoid ABCD if a = 12 cm, c = 4 cm, the length of AC is same as the length of BC and the area S of the triangle ABC is 9 cm square.
Calculate the arm length b of the trapezoid ABCD if a = 12 cm, c = 4 cm, the length of AC is same as the length of BC and the area S of the triangle ABC is 9 cm square. - Forces
 Determine the resultant of two perpendicular forces F1 = 560 N and the second force 25% smaller.
Determine the resultant of two perpendicular forces F1 = 560 N and the second force 25% smaller. - SAS calculation
 Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle A is 47°, find side a. Please round to one decimal.
Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle A is 47°, find side a. Please round to one decimal. - Equilateral triangle vs circle
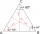 Find the area of an equilateral triangle inscribed in a circle of radius r = 9 cm. What percentage of the circle area does it occupy?
Find the area of an equilateral triangle inscribed in a circle of radius r = 9 cm. What percentage of the circle area does it occupy? - Isosceles right triangle
 Calculate the area of an isosceles right triangle whose perimeter is 810 cm.
Calculate the area of an isosceles right triangle whose perimeter is 810 cm. - Right-angled 82471
 The lengths a = 7.2 cm and b = 10.4 cm are dropped in the right-angled triangle ABC. Do the math a) lengths of the sections of the hypotenuse b) height on the hypotenuse c
The lengths a = 7.2 cm and b = 10.4 cm are dropped in the right-angled triangle ABC. Do the math a) lengths of the sections of the hypotenuse b) height on the hypotenuse c - Crossbars 80697
 Calculate the length of the middle crossbars in an isosceles triangle if the length of the arm is 52mm and the base height is 48mm
Calculate the length of the middle crossbars in an isosceles triangle if the length of the arm is 52mm and the base height is 48mm - Perpendicular 73574
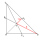 The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line.
The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line. - Hypotenuse 72524
 We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2 - Traffic sign
 There is a traffic sign for climbing on the road with an angle of 7%. Calculate at what angle the road rises (falls).
There is a traffic sign for climbing on the road with an angle of 7%. Calculate at what angle the road rises (falls). - Right Δ
 A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle.
A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle. - Perpendicular 82473
 In the right triangle KLM, the hypotenuse l = 9 cm and the perpendicular k = 6 cm. Calculate the size of the height vl and the line tk.
In the right triangle KLM, the hypotenuse l = 9 cm and the perpendicular k = 6 cm. Calculate the size of the height vl and the line tk. - Perpendicular 67174
 Calculate the perpendicular s in the right triangle STU (the right angle at the vertex U), if the hypotenuse is long u = 93cm and the perpendicular t = 48 cm
Calculate the perpendicular s in the right triangle STU (the right angle at the vertex U), if the hypotenuse is long u = 93cm and the perpendicular t = 48 cm - Diamond ABCD
 In the diamond ABCD, the diagonal e = 24 cm, and the size of angle SAB is 28 degrees, where S is the intersection of the diagonals. Calculate the circumference of the diamond.
In the diamond ABCD, the diagonal e = 24 cm, and the size of angle SAB is 28 degrees, where S is the intersection of the diagonals. Calculate the circumference of the diamond. - Measurements of a triangle
 Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
