Pythagorean theorem + diagonal - practice problems
Number of problems found: 374
- Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - Square
 Calculate the side of a square with a diagonal measurement of 10 cm.
Calculate the side of a square with a diagonal measurement of 10 cm. - Square
 Calculate the area of the square with diagonal 64 cm.
Calculate the area of the square with diagonal 64 cm. - How long
 How long is the diagonal of the square with side a = 50mm?
How long is the diagonal of the square with side a = 50mm? - The diagonal 4
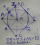 The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter.
The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter. - Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Square
 Calculate the square's perimeter and area with a diagonal length of 30 cm.
Calculate the square's perimeter and area with a diagonal length of 30 cm. - Diagonal of square
 Calculate the side of a square when its diagonal is 10 cm.
Calculate the side of a square when its diagonal is 10 cm. - Diamond side
 The diagonals of the diamond are 18 cm and 14 cm long. Calculate the length of the diamond side.
The diagonals of the diamond are 18 cm and 14 cm long. Calculate the length of the diamond side. - Circles
 The area of a circle inscribed in a square is 14. What is the area of a circle circumscribed around a square?
The area of a circle inscribed in a square is 14. What is the area of a circle circumscribed around a square? - Tv screen
 The length of its diagonal gives the size of a tv screen. If the dimension of a tv screen is 16 inches by 14 inches, what is the TV screen size?
The length of its diagonal gives the size of a tv screen. If the dimension of a tv screen is 16 inches by 14 inches, what is the TV screen size? - Diamond
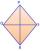 Calculate the length of the two diagonals of the diamond if: a = 13 cm v = 12 cm
Calculate the length of the two diagonals of the diamond if: a = 13 cm v = 12 cm - Median
 In the right triangle are sides a=96 dm b=31 dm. Calculate the length of the medians tc to the hypotenuse.
In the right triangle are sides a=96 dm b=31 dm. Calculate the length of the medians tc to the hypotenuse. - Circumference 3919
 Determine the diagonal of a square whose circumference is equal to 72 cm.
Determine the diagonal of a square whose circumference is equal to 72 cm. - Diagonal 2738
 ABCD square has a diagonal length of 8 cm. What is the area of the square?
ABCD square has a diagonal length of 8 cm. What is the area of the square? - Area of a rectangle
 Calculate a rectangle area with a diagonal of u = 12.5cm and a width of b = 3.5cm. Use the Pythagorean theorem.
Calculate a rectangle area with a diagonal of u = 12.5cm and a width of b = 3.5cm. Use the Pythagorean theorem. - Rhombus
 The rhombus with area 137 has one diagonal that is longer by 5 than the second one. Calculate the length of the diagonals and rhombus sides.
The rhombus with area 137 has one diagonal that is longer by 5 than the second one. Calculate the length of the diagonals and rhombus sides. - Square2
 The side of the square is a = 5.6 cm. How long is its diagonal?
The side of the square is a = 5.6 cm. How long is its diagonal? - Surrounded 36661
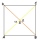 Calculate the length of the circle, which is surrounded by a square with a side length of 3 cm
Calculate the length of the circle, which is surrounded by a square with a side length of 3 cm
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
