Quadratic equation + functions - practice problems - page 2 of 9
Number of problems found: 161
- Variations 70724
 If we increase the number of elements by 2, the number of variations of the second class without repetition increases by 22. How many elements do we have initially?
If we increase the number of elements by 2, the number of variations of the second class without repetition increases by 22. How many elements do we have initially? - Combinations 70714
 If we increase the number of elements by 1, the number of combinations of the third class without repetitions increases by 10. How many elements do we have?
If we increase the number of elements by 1, the number of combinations of the third class without repetitions increases by 10. How many elements do we have? - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Graph move
 When y=2x² has moved 2 units to the left and 3 units upward, what is the graph equation?
When y=2x² has moved 2 units to the left and 3 units upward, what is the graph equation? - Finite geometric sequence
 Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =?
Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =? - The ratio 7
 The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares.
The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares. - In the
 In the arithmetic sequence, a1 = 4.8, d = 0.4. How many consecutive members, starting with the first, need to be added so that the sum is greater than 170?
In the arithmetic sequence, a1 = 4.8, d = 0.4. How many consecutive members, starting with the first, need to be added so that the sum is greater than 170? - Eq2 equations
 For each of the following problems, determine the roots of the equation. Given the roots, sketch the graph and explain how your sketch matches the roots given and the form of the equation: g(x)=36x²-12x+5 h(x)=x²-4x+20 f(x)=4x²-24x+45 p(x)=9x²-36x+40 g(x)
For each of the following problems, determine the roots of the equation. Given the roots, sketch the graph and explain how your sketch matches the roots given and the form of the equation: g(x)=36x²-12x+5 h(x)=x²-4x+20 f(x)=4x²-24x+45 p(x)=9x²-36x+40 g(x) - Two workers
 One worker makes a part 4 hours and the second 9 hours later than they would make the same part together. How long does it take for each worker to make the part himself?
One worker makes a part 4 hours and the second 9 hours later than they would make the same part together. How long does it take for each worker to make the part himself? - Equation 46771
 Insert three numbers between the roots of the equation 4x² - 17x + 4 = 0 so that they form with the given GP numbers
Insert three numbers between the roots of the equation 4x² - 17x + 4 = 0 so that they form with the given GP numbers - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Height and base
 An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base?
An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base? - Consider
 Consider all square prisms with a height of 10 cm. If x is the measurement of the base edge in cm, and y is the prism's volume in cm³. Graph the function
Consider all square prisms with a height of 10 cm. If x is the measurement of the base edge in cm, and y is the prism's volume in cm³. Graph the function - A rectangle 4
 A rectangle has an area of 300 and a perimeter of 80. What is the ratio of length and width?
A rectangle has an area of 300 and a perimeter of 80. What is the ratio of length and width? - Functions 42201
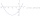 Y = x² + 4x-2 Quadratic functions Calculate and graph.
Y = x² + 4x-2 Quadratic functions Calculate and graph. - Tourists
 Tourists hire a guide. Everyone will pay the same amount. If there are two fewer of them, they will pay 14 crowns more, and if there are three more, they will pay 14 crowns less. How many tourists are there and how much have the guides paid?
Tourists hire a guide. Everyone will pay the same amount. If there are two fewer of them, they will pay 14 crowns more, and if there are three more, they will pay 14 crowns less. How many tourists are there and how much have the guides paid? - Two grandmothers
 Two grandmothers went to the market to sell eggs, and they had 100. When they sold all the eggs, they made the same money. The first grandmother said to the second, "If I sold my eggs for your price, I would earn 15 crowns. " The other grandmother replied
Two grandmothers went to the market to sell eggs, and they had 100. When they sold all the eggs, they made the same money. The first grandmother said to the second, "If I sold my eggs for your price, I would earn 15 crowns. " The other grandmother replied - Pagans
 Jano and Michael ate pagans. Jano ate three more than Michael. The product of their counts (numbers) is 180. How many pagans did each of them eat?
Jano and Michael ate pagans. Jano ate three more than Michael. The product of their counts (numbers) is 180. How many pagans did each of them eat?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
