Ratio + diagonal - practice problems
Number of problems found: 46
- Rectangular 80776
 The perimeter of the rectangular garden is 42 meters. Its sides are in the ratio 3:4. Calculate the length of the sidewalk that is the diagonal of the garden.
The perimeter of the rectangular garden is 42 meters. Its sides are in the ratio 3:4. Calculate the length of the sidewalk that is the diagonal of the garden. - The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - Calculate 70814
 The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle. - Rectangle 62854
 The aspect ratio of the rectangle and its diagonal is 9:12:15. Calculate the area of the rectangle if the length of the diagonal is 105 cm.
The aspect ratio of the rectangle and its diagonal is 9:12:15. Calculate the area of the rectangle if the length of the diagonal is 105 cm.
- The diamond
 The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond.
The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond. - Two cables
 On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag.
On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag. - Identical 35961
 Nine identical spheres are stacked in the cube to fill the volume of the cube as much as possible. What part of the volume will the cube fill?
Nine identical spheres are stacked in the cube to fill the volume of the cube as much as possible. What part of the volume will the cube fill? - Calculate 23411
 The prism with a diamond base has one base diagonal of 20 cm and a base edge of 26 cm. The edge of the base is 2:3 to the height of the prism. Calculate the volume of the prism.
The prism with a diamond base has one base diagonal of 20 cm and a base edge of 26 cm. The edge of the base is 2:3 to the height of the prism. Calculate the volume of the prism. - Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
- A rectangle 2
 A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths. - Cuboid face diagonals
 The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid.
The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid. - Ratio of sides
 Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7.
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7. - Trapezium diagonals
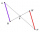 It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Rectangular 7801
 The length of the sides of the rectangular garden is 4:3. The junction of the centers of adjacent sides is 20 m long. Calculate the area of the garden.
The length of the sides of the rectangular garden is 4:3. The junction of the centers of adjacent sides is 20 m long. Calculate the area of the garden.
- Rectangular plot
 The dimensions of a rectangular plot are (x+1)m and (2x-y)m. If the sum of x and y is 3m and the plot's perimeter is 36m. Find the area of the diagonal of the plot.
The dimensions of a rectangular plot are (x+1)m and (2x-y)m. If the sum of x and y is 3m and the plot's perimeter is 36m. Find the area of the diagonal of the plot. - Rectangular field
 A rectangular field has a diagonal length of 169m. If the length and width are in the ratio of 12:5. Find the dimensions of the field, the perimeter of the field, and the area of the field.
A rectangular field has a diagonal length of 169m. If the length and width are in the ratio of 12:5. Find the dimensions of the field, the perimeter of the field, and the area of the field. - Circumference 7615
 The sides of the rectangle are in a ratio of 3:5. Its circumference is 48 cm. Calculate the length of its diagonal.
The sides of the rectangle are in a ratio of 3:5. Its circumference is 48 cm. Calculate the length of its diagonal. - Rectangular garden
 The sides of the rectangular garden are in a ratio of 1:2. The diagonal has a length of 20 meters. Calculate the area and perimeter of the garden.
The sides of the rectangular garden are in a ratio of 1:2. The diagonal has a length of 20 meters. Calculate the area and perimeter of the garden. - Ratio of edges
 The cuboid dimensions are in a ratio of 3:1:2. The body diagonal has a length of 28 cm. Find the volume of a cuboid.
The cuboid dimensions are in a ratio of 3:1:2. The body diagonal has a length of 28 cm. Find the volume of a cuboid.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
