Reason + polygon - practice problems
Number of problems found: 23
- Tetrahedron 83144
 A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise?
A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise? - Probability 81637
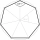 We randomly select three different points from the vertices of a regular heptagon and connect them with line segments. The probability that the resulting triangle will be isosceles is equal to: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7
We randomly select three different points from the vertices of a regular heptagon and connect them with line segments. The probability that the resulting triangle will be isosceles is equal to: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7 - Inaccessible 69794
 Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B, - Determine 69304
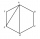 Determine the size of the ACF angle in the regular ABCDEF hexagon.
Determine the size of the ACF angle in the regular ABCDEF hexagon. - Competition 33041
 The long-term volleyball tournament is played on a one-on-one basis. So far, 11 teams have entered the competition. How many matches will be lost when two teams unsubscribe?
The long-term volleyball tournament is played on a one-on-one basis. So far, 11 teams have entered the competition. How many matches will be lost when two teams unsubscribe? - Other's 31461
 There are 13 guests at each other's party. How many clicks will you hear?
There are 13 guests at each other's party. How many clicks will you hear? - Ten persons
 Ten persons, each person, make a hand to each person. How many hands were given?
Ten persons, each person, make a hand to each person. How many hands were given? - Dodecagon
 Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees.
Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees. - Annulus
 Two concentric circles with radii 1 and 9 surround the annular circle. This ring is inscribed with n circles that do not overlap. Determine the highest possible value of n.
Two concentric circles with radii 1 and 9 surround the annular circle. This ring is inscribed with n circles that do not overlap. Determine the highest possible value of n. - Irregular pentagon
 A rectangle-shaped, 16 x 4 cm strip of paper is folded lengthwise so that the lower right corner is applied to the upper left corner. What area does the pentagon have?
A rectangle-shaped, 16 x 4 cm strip of paper is folded lengthwise so that the lower right corner is applied to the upper left corner. What area does the pentagon have? - Hexagon
 Divide a regular hexagon into lines into nine completely identical parts; none of them must be in a mirror image (you can only rotate individual parts arbitrarily).
Divide a regular hexagon into lines into nine completely identical parts; none of them must be in a mirror image (you can only rotate individual parts arbitrarily). - Each with each
 Five pupils from 3A class played table tennis. How many matches did they play with each other?
Five pupils from 3A class played table tennis. How many matches did they play with each other? - Quadrilaterals 7224
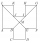 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode - Perpendicular 7223
 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M. The quadrilateral
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M. The quadrilateral - Circumference 7143
 Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci
Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci - Quadrangular 4559
 The quadrangular garden should be fenced off with a slatted fence. The sides of the orchard are 65m, 78m, 40m and 32m. The wheels are to be placed 6m apart, and the axes of the rims are 15cm apart. How much is needed for a wheel fence, and how many batten
The quadrangular garden should be fenced off with a slatted fence. The sides of the orchard are 65m, 78m, 40m and 32m. The wheels are to be placed 6m apart, and the axes of the rims are 15cm apart. How much is needed for a wheel fence, and how many batten - Candy - MO
 Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t
Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t - Octahedron - sum
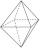 On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al
On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Hexagon rotation
 A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated?
A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated? - Hairs
 Suppose the length of the hair is affected by only the α-keratin synthesis, which is the major component. This synthesis takes place in the epithelial cells of the hair bulb. The structure of α-keratin is made up of α-helix for the 3.6 amino acid residues
Suppose the length of the hair is affected by only the α-keratin synthesis, which is the major component. This synthesis takes place in the epithelial cells of the hair bulb. The structure of α-keratin is made up of α-helix for the 3.6 amino acid residues
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
