Rectangle - practice for 14 year olds
Number of problems found: 264
- The perimeter 10
 The perimeter of a rectangle is 162 inches. The length is 35 inches longer than the width. Find the length and width of the rectangle.
The perimeter of a rectangle is 162 inches. The length is 35 inches longer than the width. Find the length and width of the rectangle. - Length and width
 The length of a rectangle is 7 cm more than the width. Find the width and length if the perimeter of the rectangle is 78 cm.
The length of a rectangle is 7 cm more than the width. Find the width and length if the perimeter of the rectangle is 78 cm. - Rectangle - general expression
 Find the area of a rectangle whose width is x-2 units and length of x+4 units.
Find the area of a rectangle whose width is x-2 units and length of x+4 units. - The ratio 10
 The ratio of length and breadth of a rectangular park is 3:2, and its perimeter is 150m. Find its area.
The ratio of length and breadth of a rectangular park is 3:2, and its perimeter is 150m. Find its area. - A blanket
 A blanket is 60 inches by 72 inches. If you want to make it 1/3 smaller, what size would it be?
A blanket is 60 inches by 72 inches. If you want to make it 1/3 smaller, what size would it be? - Jackie 2
 Jackie bought an equal number of tulip bulbs and daffodil bulbs. Along the length of her garden, Jackie planted 6 daffodil bulbs and 3 tulip bulbs per foot. She has 5 daffodil bulbs and 29 tulip bulbs remaining to plant elsewhere. How long is Jackie's gar
Jackie bought an equal number of tulip bulbs and daffodil bulbs. Along the length of her garden, Jackie planted 6 daffodil bulbs and 3 tulip bulbs per foot. She has 5 daffodil bulbs and 29 tulip bulbs remaining to plant elsewhere. How long is Jackie's gar - Coordinates - rectangle
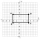 Find the perimeter of the rectangle with vertices A(1,4), B (1,0 ), C (4,0), D (4,4 )
Find the perimeter of the rectangle with vertices A(1,4), B (1,0 ), C (4,0), D (4,4 ) - Polynomial rectangle
 If the length and width of a rectangle are (a² - 6a + 4) and ( -2a² - 9a + 3), find the area of the rectangle.
If the length and width of a rectangle are (a² - 6a + 4) and ( -2a² - 9a + 3), find the area of the rectangle. - Harold
 Harold made a rectangular dog run in his backyard. The area of the dog run is 96 square feet. What are three different possible dimensions of dog run?
Harold made a rectangular dog run in his backyard. The area of the dog run is 96 square feet. What are three different possible dimensions of dog run? - Width and length
 For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle? - A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - Rectangle Anton
 The difference between the length and width of the rectangle is 8. Length is 3-times larger than the width. Calculate the dimensions of the rectangle.
The difference between the length and width of the rectangle is 8. Length is 3-times larger than the width. Calculate the dimensions of the rectangle. - Dimensions 81780
 The garden is 24m long and 15m wide. Determine the ratio of the dimensions of this rectangle.
The garden is 24m long and 15m wide. Determine the ratio of the dimensions of this rectangle. - Length 9
 The length of a rectangle is 8 meters smaller than twice of breadth. If the perimeter of the rectangle is 50, find its length and breadth.
The length of a rectangle is 8 meters smaller than twice of breadth. If the perimeter of the rectangle is 50, find its length and breadth. - Dimensions of rectangle
 Find the dimensions of a rectangle, given that its perimeter is 110 cm. Its length is 1 cm, more than twice its width.
Find the dimensions of a rectangle, given that its perimeter is 110 cm. Its length is 1 cm, more than twice its width. - Rectangular 9401
 Matrix E is a rectangular matrix that contains 48 elements and four rows. How many columns does this matrix have?
Matrix E is a rectangular matrix that contains 48 elements and four rows. How many columns does this matrix have? - Dimensions 3
 A perimeter of a rectangular field is 96 meters. The length is four meters less than three times the width. Find the length and width (its dimensions).
A perimeter of a rectangular field is 96 meters. The length is four meters less than three times the width. Find the length and width (its dimensions). - The length 4
 The length of a rectangular room measures twice a number x increased by 5. The width measures a number x increased by 3. What is the perimeter of the room?
The length of a rectangular room measures twice a number x increased by 5. The width measures a number x increased by 3. What is the perimeter of the room? - The length
 The length of a rectangle is 6 meters, less than twice the width. If the area of the rectangle is 216 meters, find the rectangle's dimensions.
The length of a rectangle is 6 meters, less than twice the width. If the area of the rectangle is 216 meters, find the rectangle's dimensions. - Perimeter of a rectangle
 If the perimeter of a rectangle is 114 meters and the length is twice the width plus 6 meters, what are the length and width?
If the perimeter of a rectangle is 114 meters and the length is twice the width plus 6 meters, what are the length and width?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
