Right triangle - practice for 14 year olds - page 37 of 53
Number of problems found: 1043
- R Trapezium
 Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter?
Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter? - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - Triangular 6610
 The shell of the rotating cylinder is four times larger than the contents of its base. Determine the volume of the regular triangular prism inscribed in the cylinder. The radius of the bottom of the cylinder is 10 cm.
The shell of the rotating cylinder is four times larger than the contents of its base. Determine the volume of the regular triangular prism inscribed in the cylinder. The radius of the bottom of the cylinder is 10 cm. - The roof
 The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste.
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - Pyramid
 The pyramid has a base rectangle with a = 6cm, b = 8cm. The side edges are the same, and their length is 12.5 cm. Calculate the surface of the pyramid.
The pyramid has a base rectangle with a = 6cm, b = 8cm. The side edges are the same, and their length is 12.5 cm. Calculate the surface of the pyramid. - Diagonals 82850
 How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other?
How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other? - Elevation
 What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km. - Northeast 66694
 Katka and Honza rode out on their scooters at the same time. Katka drove at a speed of 4.5 km/30 min, and Honza drove at a speed of 4 km/20 min. a) how many m did they travel in 2 minutes if they went in the opposite direction? b) how many miles did they
Katka and Honza rode out on their scooters at the same time. Katka drove at a speed of 4.5 km/30 min, and Honza drove at a speed of 4 km/20 min. a) how many m did they travel in 2 minutes if they went in the opposite direction? b) how many miles did they - Hexagon
 There is a regular hexagon ABCDEF. If the area of the triangle ABC is 22, what is the area of the hexagon ABCDEF? I do not know how to solve it simply....
There is a regular hexagon ABCDEF. If the area of the triangle ABC is 22, what is the area of the hexagon ABCDEF? I do not know how to solve it simply.... - Rectangular 5798
 The pyramid has a rectangular base with dimensions a = 5cm, b = 6cm. The side edges are identical; their length is h = 11cm. Calculate the surface of the pyramid.
The pyramid has a rectangular base with dimensions a = 5cm, b = 6cm. The side edges are identical; their length is h = 11cm. Calculate the surface of the pyramid. - Body diagonal
 Calculate the length of the body diagonal of the 6cm cube.
Calculate the length of the body diagonal of the 6cm cube. - Laths
 There are two laths in the garage opposite one another: one 2 meters long and the other 3 meters long. They fall against each other and lean against the opposite walls of the garage. Both laths touch at 70 cm above the garage floor. How wide is the garage
There are two laths in the garage opposite one another: one 2 meters long and the other 3 meters long. They fall against each other and lean against the opposite walls of the garage. Both laths touch at 70 cm above the garage floor. How wide is the garage - Water channel
 The cross-section of the water channel is a trapezoid. The bottom width is 19.7 m, the water surface width is 28.5 m, and the side walls have a slope of 67°30' and 61°15'. Calculate how much water flows through the channel in 5 minutes if the water flows
The cross-section of the water channel is a trapezoid. The bottom width is 19.7 m, the water surface width is 28.5 m, and the side walls have a slope of 67°30' and 61°15'. Calculate how much water flows through the channel in 5 minutes if the water flows - The ditch
 Ditch with a cross-section of an isosceles trapezoid with bases 2m and 6m deep 1.5m. How long is the slope of the ditch?
Ditch with a cross-section of an isosceles trapezoid with bases 2m and 6m deep 1.5m. How long is the slope of the ditch? - Cap
 A rotating cone shapes a jesters hat. Calculate how much paper is needed for the cap 54 cm high when the head circumference is 47 cm.
A rotating cone shapes a jesters hat. Calculate how much paper is needed for the cap 54 cm high when the head circumference is 47 cm. - Leg
 Determine the trapezoid area with bases 32 and 12; the height is 2 shorter than its leg.
Determine the trapezoid area with bases 32 and 12; the height is 2 shorter than its leg. - The quadrilateral
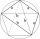 The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right.
The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right. - Triangle IRT
 An isosceles right triangle ABC with right angle at vertex C has vertex coordinates: A (-1, 2); C (-5, -2). Calculate the length of segment AB.
An isosceles right triangle ABC with right angle at vertex C has vertex coordinates: A (-1, 2); C (-5, -2). Calculate the length of segment AB. - The trapezium
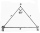 The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium.
The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium. - The pyramid 4s
 The pyramid with a rectangular base measuring 6 dm and 8 dm has a side edge of a length of 13 dm. Calculate the surface area and volume of this pyramid.
The pyramid with a rectangular base measuring 6 dm and 8 dm has a side edge of a length of 13 dm. Calculate the surface area and volume of this pyramid.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
