Right triangle + prism - practice problems - page 2 of 7
Number of problems found: 123
- 3s prism
 It is given a regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm. Calculate the volume of the prism.
It is given a regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm. Calculate the volume of the prism. - 3sides prism
 The base of a vertical prism is an isosceles triangle whose base is 10 cm, and the arm is 13 cm long. Prism height is three times the height of the base triangle. Calculate the surface area of the prism.
The base of a vertical prism is an isosceles triangle whose base is 10 cm, and the arm is 13 cm long. Prism height is three times the height of the base triangle. Calculate the surface area of the prism. - Perpendicular 3146
 The base of the vertical prism is a right triangle with a perpendicular 5 cm. The area of the largest wall is 130 cm2, and the body's height is 10 cm. Calculate the surface area of the body.
The base of the vertical prism is a right triangle with a perpendicular 5 cm. The area of the largest wall is 130 cm2, and the body's height is 10 cm. Calculate the surface area of the body. - Calculate 31991
 Calculate the volume and surface of a prism whose height is 16 cm, and the base is in the shape of a right triangle with 5cm and 12cm trunks and a 13cm diaphragm.
Calculate the volume and surface of a prism whose height is 16 cm, and the base is in the shape of a right triangle with 5cm and 12cm trunks and a 13cm diaphragm.
- Perpendicular prism
 Calculate the volume of the vertical prism if its height is 60.8 cm and the base is a rectangular triangle with 40.4 cm and 43 cm legs.
Calculate the volume of the vertical prism if its height is 60.8 cm and the base is a rectangular triangle with 40.4 cm and 43 cm legs. - Measures 23791
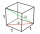 The volume of the block is 144 cm³. The base measures 3 cm and 4 cm. How big is the body diagonal?
The volume of the block is 144 cm³. The base measures 3 cm and 4 cm. How big is the body diagonal? - Right-angled triangle base
 Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of a prism is 24 cm.
Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of a prism is 24 cm. - A box
 A box is 15 centimeters long, 4 centimeters wide, and 3 centimeters tall. What is the diagonal S of the bottom side? What is the length of the body diagonal R?
A box is 15 centimeters long, 4 centimeters wide, and 3 centimeters tall. What is the diagonal S of the bottom side? What is the length of the body diagonal R? - Triangular 6345
 Calculate the volume and surface of a triangular prism whose base is a right triangle with sides a = 3m, b = Va = 4m, and c = 5m. The height of the prism is v = 5.5 m.
Calculate the volume and surface of a triangular prism whose base is a right triangle with sides a = 3m, b = Va = 4m, and c = 5m. The height of the prism is v = 5.5 m.
- The gable
 The house's gable has the shape of an isosceles triangle, which has a base length of 14 meters, and arms with a length of 8 meters. What is the tall gable of the house?
The house's gable has the shape of an isosceles triangle, which has a base length of 14 meters, and arms with a length of 8 meters. What is the tall gable of the house? - Triangular 6950
 A triangular prism has the base of a right triangle with 6 dm and 8 dm legs and a hypotenuse of 10 dm. The height of the prism is 40 dm. What is the volume of a prism?
A triangular prism has the base of a right triangle with 6 dm and 8 dm legs and a hypotenuse of 10 dm. The height of the prism is 40 dm. What is the volume of a prism? - ----------------- 4850
 v = 35 m α = 55 ° β = 15 ° ----------------- X =? Calculate: V- barrack volume =? S- barrack area =?
v = 35 m α = 55 ° β = 15 ° ----------------- X =? Calculate: V- barrack volume =? S- barrack area =? - Wall and body diagonals
 The block/cuboid has dimensions a = 4cm, b = 3cm, and c = 12cm. Calculate the length of the wall and body diagonals.
The block/cuboid has dimensions a = 4cm, b = 3cm, and c = 12cm. Calculate the length of the wall and body diagonals. - Consumption 4259
 What is the consumption of fabric per tent: Length 250, width 180, the height of triangle 120, sides 150 (all cm). What is the volume of air in the tent?
What is the consumption of fabric per tent: Length 250, width 180, the height of triangle 120, sides 150 (all cm). What is the volume of air in the tent?
- Perpendicular 3482
 The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle.
The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle. - The block
 The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block.
The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block. - Perpendicular 6624
 A = 3 cm b = 4 cm prism height h = 10cm Calculate the volume of a triangular prism with the base of a right triangle - the perpendicular a, b.
A = 3 cm b = 4 cm prism height h = 10cm Calculate the volume of a triangular prism with the base of a right triangle - the perpendicular a, b. - Triangular 2715
 Determine the volume and surface of a triangular prism with a height of 12.4 cm; the base is a right triangle with 6 cm and 8 cm.
Determine the volume and surface of a triangular prism with a height of 12.4 cm; the base is a right triangle with 6 cm and 8 cm. - Height of the room
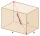 Given the floor area of a room as 24 feet by 48 feet and the space diagonal of a room as 56 feet. Can you find the height of the room?
Given the floor area of a room as 24 feet by 48 feet and the space diagonal of a room as 56 feet. Can you find the height of the room?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
