Right triangle + volume - practice problems - page 3 of 15
Number of problems found: 289
- Solid cuboid
 A solid cuboid has a volume of 40 cm³. The cuboid has a total surface area of 100 cm squared. One edge of the cuboid has a length of 2 cm. Find the length of a diagonal of the cuboid. Give your answer correct to 3 sig. Fig.
A solid cuboid has a volume of 40 cm³. The cuboid has a total surface area of 100 cm squared. One edge of the cuboid has a length of 2 cm. Find the length of a diagonal of the cuboid. Give your answer correct to 3 sig. Fig. - Perpendiculars 17003
 What is the hole volume drilled by the drill in the shape of a right triangle that revolves around a longer perpendicular? The perpendiculars of the triangle are 10 cm and 3 cm long.
What is the hole volume drilled by the drill in the shape of a right triangle that revolves around a longer perpendicular? The perpendiculars of the triangle are 10 cm and 3 cm long. - Prism height
 What is the prism's height with the base of a right triangle of 6 cm and 9 cm? The diaphragm is 10.8 cm long. The volume of the prism is 58 cm³. Calculate its surface.
What is the prism's height with the base of a right triangle of 6 cm and 9 cm? The diaphragm is 10.8 cm long. The volume of the prism is 58 cm³. Calculate its surface. - Angle of cone
 The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone.
The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone. - Body diagonal
 Calculate the volume of a cuboid whose body diagonal u equals 6.1 cm. The rectangular base has dimensions of 3.2 cm and 2.4 cm.
Calculate the volume of a cuboid whose body diagonal u equals 6.1 cm. The rectangular base has dimensions of 3.2 cm and 2.4 cm. - Pile of sand
 A large pile of sand has been dumped into a conical pile in a warehouse. The slant height of the pile is 20 feet. The diameter of the base of the sandpile is 31 feet. Find the volume of the pile of sand.
A large pile of sand has been dumped into a conical pile in a warehouse. The slant height of the pile is 20 feet. The diameter of the base of the sandpile is 31 feet. Find the volume of the pile of sand. - Body diagonal
 Calculate the cube volume, whose body diagonal size is 75 dm. Draw a picture and highlight the body diagonally.
Calculate the cube volume, whose body diagonal size is 75 dm. Draw a picture and highlight the body diagonally. - Sphere and cone
 Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone?
Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone? - Cone
 Calculate the volume and surface area of the cone with a diameter of the base d=15 cm and the side of the cone with the base has angle 52°.
Calculate the volume and surface area of the cone with a diameter of the base d=15 cm and the side of the cone with the base has angle 52°. - Surface 19383 cone
 The volume of a cone with a radius of 6 cm is 301.44 cm cubic. What is its surface?
The volume of a cone with a radius of 6 cm is 301.44 cm cubic. What is its surface? - Frustrum - volume, area
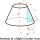 Calculate the surface and volume of the truncated cone. The radius of the smaller figure is 4 cm, the height of the cone is 4 cm, and the side of the truncated cone is 5 cm.
Calculate the surface and volume of the truncated cone. The radius of the smaller figure is 4 cm, the height of the cone is 4 cm, and the side of the truncated cone is 5 cm. - Wall height
 Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm.
Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm. - Slant height 2
 A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid. - Surface area and volume
 Find the surface area and volume of a rotating cone whose diameter is 60 mm and side length 3.4 cm.
Find the surface area and volume of a rotating cone whose diameter is 60 mm and side length 3.4 cm. - Calculate
 Calculate the cone's surface and volume from the rotation of the right triangle ABC with the squares 6 cm and 9 cm long around the shorter squeegee.
Calculate the cone's surface and volume from the rotation of the right triangle ABC with the squares 6 cm and 9 cm long around the shorter squeegee. - Triangular prism
 The perpendicular triangular prism is a right triangle with a 5 cm leg. The prism's largest wall area is 130 cm2, and the body height is 10 cm. Calculate the body volume.
The perpendicular triangular prism is a right triangle with a 5 cm leg. The prism's largest wall area is 130 cm2, and the body height is 10 cm. Calculate the body volume. - 3s prism
 It is given a regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm. Calculate the volume of the prism.
It is given a regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm. Calculate the volume of the prism. - Pyramid 4sides
 Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long and the pyramid's height is 7 cm.
Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long and the pyramid's height is 7 cm. - Calculate 31991
 Calculate the volume and surface of a prism whose height is 16 cm, and the base is in the shape of a right triangle with 5cm and 12cm trunks and a 13cm diaphragm.
Calculate the volume and surface of a prism whose height is 16 cm, and the base is in the shape of a right triangle with 5cm and 12cm trunks and a 13cm diaphragm. - Perpendicular prism
 Calculate the volume of the vertical prism if its height is 60.8 cm and the base is a rectangular triangle with 40.4 cm and 43 cm legs.
Calculate the volume of the vertical prism if its height is 60.8 cm and the base is a rectangular triangle with 40.4 cm and 43 cm legs.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
