Solid geometry + reason - practice problems
Number of problems found: 61
- Brick wall
 A garden 70 m long and 48 m wide should surround by a wall 2.1 meters high and 30 cm thick. The bricklayer will build a wall on the garden ground. How many will we need if 300 bricks are required for approximately one m³?
A garden 70 m long and 48 m wide should surround by a wall 2.1 meters high and 30 cm thick. The bricklayer will build a wall on the garden ground. How many will we need if 300 bricks are required for approximately one m³? - Workers
 Workers are digging a jump pit in the schoolyard. The pit has a cuboid shape with a length of 5 m, a width of 20 dm, and a depth of 36 cm. They excavate 0.4 cubic meters of soil an hour. How much time (hours and minutes) is needed to excavate this pit?
Workers are digging a jump pit in the schoolyard. The pit has a cuboid shape with a length of 5 m, a width of 20 dm, and a depth of 36 cm. They excavate 0.4 cubic meters of soil an hour. How much time (hours and minutes) is needed to excavate this pit? - Leveling
 Calculate how many we must purchase 25 kg bags of leveling concrete if we level room 15 m² to the "height" 6 mm if consumption is 1.5 kg per square meter and millimeter thickness.
Calculate how many we must purchase 25 kg bags of leveling concrete if we level room 15 m² to the "height" 6 mm if consumption is 1.5 kg per square meter and millimeter thickness. - Gutter
 How much metal is needed to produce 60 pieces of gutter pipes with the diameter 17 cm and length of 6 m? The plate bends add 6% of the material.
How much metal is needed to produce 60 pieces of gutter pipes with the diameter 17 cm and length of 6 m? The plate bends add 6% of the material. - Dimensions 80753
 We color a wooden block with dimensions a = 4 cm, b = 3 cm, c = 2 cm and then cut it into cubes of 1 cm³. How many cats will she have? a) just one wall painted b) just two walls stained c) just three walls painted d) no painted wall?
We color a wooden block with dimensions a = 4 cm, b = 3 cm, c = 2 cm and then cut it into cubes of 1 cm³. How many cats will she have? a) just one wall painted b) just two walls stained c) just three walls painted d) no painted wall? - Barrel 2
 The empty barrel weighs 7 kg. When it is filled with water up to 45% height, it weighs 60 kg. How heavy is a barrel full of water?
The empty barrel weighs 7 kg. When it is filled with water up to 45% height, it weighs 60 kg. How heavy is a barrel full of water? - Sugar - cuboid
 Pablo received from his master a cuboid composed of identical sugar cubes with a count between 1000 and 2000. The Pejko eat sugar cubes in layers. On the first day, eat one layer from the front. On the second day, one layer from the right, and on the thir
Pablo received from his master a cuboid composed of identical sugar cubes with a count between 1000 and 2000. The Pejko eat sugar cubes in layers. On the first day, eat one layer from the front. On the second day, one layer from the right, and on the thir - Barrel 3
 Barrel with water weights 118 kg. When we get off 75% of water, it weighs 35 kg. How many kg has an empty barrel?
Barrel with water weights 118 kg. When we get off 75% of water, it weighs 35 kg. How many kg has an empty barrel? - Water container
 The container with water weighs 1.48 kg when we cast 75% of the water content of water weight 0.73 kg. How heavy is an empty container?
The container with water weighs 1.48 kg when we cast 75% of the water content of water weight 0.73 kg. How heavy is an empty container? - Carefully 12791
 Spruce logs with a diameter of 270 mm and a length of 4 m are carefully loaded onto a wagon with a bed width of 2,700 mm and stacked in 9 layers. How much does such a load of spruce wood weigh if its density is 700 kg/m³?
Spruce logs with a diameter of 270 mm and a length of 4 m are carefully loaded onto a wagon with a bed width of 2,700 mm and stacked in 9 layers. How much does such a load of spruce wood weigh if its density is 700 kg/m³? - Bracelet 70684
 A gold ring with a width of 1 cm is made by drilling a sphere with a radius of 1 cm through its center. A gold bracelet with a width of 1 cm is made by drilling a sphere with a radius of 4 cm through its center. Which piece of jewelry will be worth more i
A gold ring with a width of 1 cm is made by drilling a sphere with a radius of 1 cm through its center. A gold bracelet with a width of 1 cm is made by drilling a sphere with a radius of 4 cm through its center. Which piece of jewelry will be worth more i - Five-sevenths 4789
 Forty-two liters of water fill the barrel to two-thirds of its volume. How many liters of water do we need to add if it is filled to five-sevenths of a volume?
Forty-two liters of water fill the barrel to two-thirds of its volume. How many liters of water do we need to add if it is filled to five-sevenths of a volume? - Sphere cut
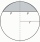 A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - 2x cone
 Circular cone height 84 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone.
Circular cone height 84 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - No smoke
 Tobacco company NO-SMOKE adorned its stand at the cigarette-type trade fair with cigarette-shaped. The dimensions of which were 20 times the size of a regular cigarette. Regular cigarette contains 0.8 mg of nicotine. How much nicotine would a giant cigare
Tobacco company NO-SMOKE adorned its stand at the cigarette-type trade fair with cigarette-shaped. The dimensions of which were 20 times the size of a regular cigarette. Regular cigarette contains 0.8 mg of nicotine. How much nicotine would a giant cigare - Cone-shaped 8170
 How many cone-shaped cones will we have to take to fill 20 l of creams (to the brim) if the cone has an inner base diameter of 6 cm and a height of 8 cm. Make a drawing, and write the answer.
How many cone-shaped cones will we have to take to fill 20 l of creams (to the brim) if the cone has an inner base diameter of 6 cm and a height of 8 cm. Make a drawing, and write the answer. - Integer cube
 The length of the cube edge is an integer. Its volume is in cm3, a five-digit number divisible by 1331. What is the length of the edge of this cube?
The length of the cube edge is an integer. Its volume is in cm3, a five-digit number divisible by 1331. What is the length of the edge of this cube? - Dimensions 7912
 How many blocks have integer dimensions of the edges of the surface is 48 m²?
How many blocks have integer dimensions of the edges of the surface is 48 m²? - Diameter 81760
 Winding drum length 180mm, initial diameter 60mm. Using a 6mm rope with a length of 50m, what will be the diameter of the wound drum with the rope?
Winding drum length 180mm, initial diameter 60mm. Using a 6mm rope with a length of 50m, what will be the diameter of the wound drum with the rope? - Precisely 64114
 We painted a wooden cube with an edge 4 cm long with green paint over the entire surface. Then we cut it into small cubes with an edge length of 1 cm. The number of cubes that have precisely two faces colored green is:
We painted a wooden cube with an edge 4 cm long with green paint over the entire surface. Then we cut it into small cubes with an edge length of 1 cm. The number of cubes that have precisely two faces colored green is:
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
