Square root - high school - practice problems
Number of problems found: 361
- Correct mean and CV
 For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati
For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati - Using 4
 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - Squared deviation
 Given the data from the problem (sample data: 23, 27, 35, 44), find the sum of the squared deviations (the numerator of the fraction under the square root in the formula). In finding the number, round all calculations to 2 decimals (if you carry more or f
Given the data from the problem (sample data: 23, 27, 35, 44), find the sum of the squared deviations (the numerator of the fraction under the square root in the formula). In finding the number, round all calculations to 2 decimals (if you carry more or f - The intensity
 The light intensity on a screen is inversely proportional to the square of the distance between the screen and the light source. If a screen is illuminated by a light source 20 m away, the intensity is one-fifth of what is required. Where should the light
The light intensity on a screen is inversely proportional to the square of the distance between the screen and the light source. If a screen is illuminated by a light source 20 m away, the intensity is one-fifth of what is required. Where should the light - Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - Z-score calc
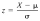 What is the Z Score for the following numbers: X is 16, and data for the population mean, and the standard deviation is 196, 193, 79, 30, 29, 81, 25, 21, 164 Level of difficulty = 2 of 2 Please format it to 2 decimal places.
What is the Z Score for the following numbers: X is 16, and data for the population mean, and the standard deviation is 196, 193, 79, 30, 29, 81, 25, 21, 164 Level of difficulty = 2 of 2 Please format it to 2 decimal places. - The length 17
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - A group
 A group of young men decides to raise ksh 480,000 to start a business. Before the actual payment was made, four members pulled out, and each of the remaining had to pay an additional ksh 20,000. Determine the original number of members.
A group of young men decides to raise ksh 480,000 to start a business. Before the actual payment was made, four members pulled out, and each of the remaining had to pay an additional ksh 20,000. Determine the original number of members. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - The coordinates 3
 The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex?
The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex? - Triangle 82
 Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR?
Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR? - Line segment
 Find the length of the line joining points A(-4,8) and B(-1,4).
Find the length of the line joining points A(-4,8) and B(-1,4). - Economic order quantity
 Annual demand for a component is 20 000 units per year. Storage cost per unit per year is £8, and each order costs £200. What is the company’s economic order quantity?
Annual demand for a component is 20 000 units per year. Storage cost per unit per year is £8, and each order costs £200. What is the company’s economic order quantity? - The Uniform Distribution
 The number of tickets purchased by an individual for Beckham colleges holiday music festival is uniformly distributed random variable ranging from 5 to 12. What is the standard deviation?
The number of tickets purchased by an individual for Beckham colleges holiday music festival is uniformly distributed random variable ranging from 5 to 12. What is the standard deviation? - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - Calculate 83160
 Calculate the distance of point A[ 4; 2; -3 ] from the plane : 2x - 2y + z + 5 = 0
Calculate the distance of point A[ 4; 2; -3 ] from the plane : 2x - 2y + z + 5 = 0 - Overhangs 83158
 The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b.
The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b. - Function: 83053
 The inverse function to the function f(x) = √(x-3) for x ≥ 3 is the function:
The inverse function to the function f(x) = √(x-3) for x ≥ 3 is the function:
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
