Square root + third power - practice problems
Number of problems found: 39
- Perfect square or cube
Would you classify 324 as a perfect square, perfect cube, both, or neither? ... - Original model
When drying, the modeling mass loses 36% of its original volume. If the cube's volume is 5.12 dm³ after drying, what was the original length of the edge? - Smallest z9
Find the smallest positive numbers a and b for which 7a³ = 11b⁵ - Smallest 79434
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
- Evaluate 26
Evaluate square root: √1³+2³+3³+4³= - Seventh term
The first term of a geometric sequence is nine, and the third term is 1296. Find the seventh term. - Liters 44041
What is the length of the edge of a cube with a volume of V = 1728 liters? - Cube-shaped box
The cube-shaped box is filled to the brim with 2 liters of milk. Calculate the box's edge and surface area. - Cube V2S
The volume of the cube is 27 dm cubic. Calculate the surface of the cube.
- Millimeter 30041
Calculate the length of the wall diagonal of a cube with a volume of 7.40 dm cubic. Express the result to the nearest millimeter. - Ball-shaped 28481
How many square meters of material is needed to make a ball-shaped balloon with a volume of 950 m³? - Derivative problem
The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal. - Equilateral cone
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Cube surfce2volume
Calculate the volume of the cube if its surface is 150 cm².
- Cuboid to cube A cuboid with dimensions of 9 cm, 6 cm, and 4 cm has the same volume as a cube. Calculate the surface of this cube.
- Magnified cube
If the lengths of the cube's edges are extended by 5 cm, its volume will increase by 485 cm³. Determine the surface of both the original and the magnified cube. - Original 18203
There is a cube with an edge. How long must the cube's edge be in which the volume should be twice the volume of the original cube? - Probability 17013
What is the probability that a randomly written two-digit number from number 20 to number 99 will be divisible by 11, the power of number 3, or a prime number? - One third power
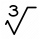Which equation justifies why ten to the one-third power equals the cube root of ten?
Find the length of the edge of a cube with a cm² surface and a volume in cm³ expressed by the same number.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
