Square + cube - practice problems
Number of problems found: 202
- Perfect square or cube
 Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
Would you classify 324 as a perfect square, perfect cube, both, or neither? ... - Determine 3888
 Determine the sum of the three-third roots of the number 64.
Determine the sum of the three-third roots of the number 64. - Determine 3873
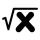 Determine the ratio of the square root of number 27 and the square root of number 16.
Determine the ratio of the square root of number 27 and the square root of number 16. - Sq and cube
 Find the product of the square of (1/2) and the cube of (2/3)
Find the product of the square of (1/2) and the cube of (2/3)
- Much 37741
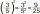 How much is half the half the cube half?
How much is half the half the cube half? - Root
 Use the law of square roots: cbrt (sqrt[2] (sqrt[4] (6))) = sqrt[n] (6)
Use the law of square roots: cbrt (sqrt[2] (sqrt[4] (6))) = sqrt[n] (6) - Three members GP
 The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers.
The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers. - Power
 Number left(sqrt(14 * sqrt[ 4 ] (14)) right) 17 can be written in the form 14^x. Find the value of x.
Number left(sqrt(14 * sqrt[ 4 ] (14)) right) 17 can be written in the form 14^x. Find the value of x. - Smallest 79434
 Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
- Six speeds
 A drilling machine is to have six speeds ranging from 50 to 750 revolutions per minute. If the speed forms a geometric progression, determine their values.
A drilling machine is to have six speeds ranging from 50 to 750 revolutions per minute. If the speed forms a geometric progression, determine their values. - One third power
 Which equation justifies why ten to the one-third power equals the cube root of ten?
Which equation justifies why ten to the one-third power equals the cube root of ten? - Derivative problem
 The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal.
The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal. - Increases 81991
 What % of bacteria will increase hourly if the number increases from 100,000 to 370,000 in 5 hours?
What % of bacteria will increase hourly if the number increases from 100,000 to 370,000 in 5 hours? - Equation 46771
 Insert three numbers between the roots of the equation 4x² - 17x + 4 = 0 so that they form with the given GP numbers
Insert three numbers between the roots of the equation 4x² - 17x + 4 = 0 so that they form with the given GP numbers
- Probability 17013
 What is the probability that a randomly written two-digit number from number 20 to number 99 will be divisible by 11, the power of number 3, or a prime number?
What is the probability that a randomly written two-digit number from number 20 to number 99 will be divisible by 11, the power of number 3, or a prime number? - Four-thirds 3852
 Anton said: I have a natural number x. I'll get three times as much if I increase it to four-thirds. What number did Anton mean?
Anton said: I have a natural number x. I'll get three times as much if I increase it to four-thirds. What number did Anton mean? - Population 37561
 The population increased from 29,000 to 31,500 in 5 years. Calculate the average annual population growth in%.
The population increased from 29,000 to 31,500 in 5 years. Calculate the average annual population growth in%. - Annual growth
 The population has grown from 25,000 to 33,600 in 10 years. Calculate what the average annual population growth in% was.
The population has grown from 25,000 to 33,600 in 10 years. Calculate what the average annual population growth in% was. - Profit growth
 A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years periods.
A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years periods.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
