The right triangle altitude theorem - high school - practice problems
Number of problems found: 56
- Euclid2
 The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle.
The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle. - Isosceles IV
 In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - Height of right RT
 The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle?
The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle? - Leg and height
 Solve right triangle with height v = 9.6 m and shorter cathetus b = 17.3 m.
Solve right triangle with height v = 9.6 m and shorter cathetus b = 17.3 m.
- Euklid4
 The legs of a right triangle have dimensions 244 m and 246 m. Calculate the length of the hypotenuse and the height of this right triangle.
The legs of a right triangle have dimensions 244 m and 246 m. Calculate the length of the hypotenuse and the height of this right triangle. - Hypotenuse and height
 In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs.
In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs. - Euclid 5
 Calculate the length of remain sides of a right triangle ABC if a = 7 cm and height vc = 5 cm.
Calculate the length of remain sides of a right triangle ABC if a = 7 cm and height vc = 5 cm. - Triangle ABC
 Right triangle ABC with right angle at the C, |BC|=19, |AB|=32. Calculate the height of the triangle hAB to the side AB.
Right triangle ABC with right angle at the C, |BC|=19, |AB|=32. Calculate the height of the triangle hAB to the side AB. - Euclid3
 Calculate the height and sides of the right triangle if one leg is a = 81 cm and the section of hypotenuse adjacent to the second leg cb = 39 cm.
Calculate the height and sides of the right triangle if one leg is a = 81 cm and the section of hypotenuse adjacent to the second leg cb = 39 cm.
- Proof PT
 Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it.
Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it. - Area of RT
 The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle.
The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle. - Euclid1
 The right triangle has hypotenuse c = 27 cm. How large sections cuts height hc=3 cm on the hypotenuse c?
The right triangle has hypotenuse c = 27 cm. How large sections cuts height hc=3 cm on the hypotenuse c? - RT triangle and height
 Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm.
Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm. - Without Euclid laws
 Right triangle ABC with a right angle at the C has a=14 and hypotenuse c=26. Calculate the height h of this triangle without the use of Euclidean laws.
Right triangle ABC with a right angle at the C has a=14 and hypotenuse c=26. Calculate the height h of this triangle without the use of Euclidean laws.
- Area of RT
 Calculate the right triangle area that hypotenuse has length 14, and one hypotenuse segment has length 5.
Calculate the right triangle area that hypotenuse has length 14, and one hypotenuse segment has length 5. - RT - hypotenuse and altitude
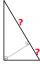 The right triangle BTG has hypotenuse g=117 m, and the altitude to g is 54 m. How long are hypotenuse segments?
The right triangle BTG has hypotenuse g=117 m, and the altitude to g is 54 m. How long are hypotenuse segments? - Euclidean distance
 Calculate the Euclidean distance between shops A, B, and C, where: A 45 0.05 B 60 0.05 C 52 0.09 The first figure is the weight in grams of bread, and the second figure is the USD price.
Calculate the Euclidean distance between shops A, B, and C, where: A 45 0.05 B 60 0.05 C 52 0.09 The first figure is the weight in grams of bread, and the second figure is the USD price. - Sides of the triangle
 Calculate triangle sides where its area is S = 84 cm² and a = x, b = x + 1, xc = x + 2
Calculate triangle sides where its area is S = 84 cm² and a = x, b = x + 1, xc = x + 2 - RT sides
 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
