Volume - practice for 13 year olds
Number of problems found: 1009
- Water per day
 Liam's goal is to drink 12 cups of water a day. So far, Liam has drank one-half gallon of water today. How much more water, in OUNCES, does Liam need to drink today to reach his goal of 12 cups of water per day?
Liam's goal is to drink 12 cups of water a day. So far, Liam has drank one-half gallon of water today. How much more water, in OUNCES, does Liam need to drink today to reach his goal of 12 cups of water per day? - Grain storage
 On their farm, Adam’s family maintains a storage that can hold 19.2 cubic yards (yd3) of grain. Use the fact that 1 yard is approximately equal to 0.9144 m to convert this volume to m³.
On their farm, Adam’s family maintains a storage that can hold 19.2 cubic yards (yd3) of grain. Use the fact that 1 yard is approximately equal to 0.9144 m to convert this volume to m³. - Vidya
 Vidya and Peter went for a picnic . Their mother gave them a water bottle that contained 5 liters of water. Vidya consumed 2/5 of the water. Peter consumed the remaining water. How much water did Vidya drink? How much water did Peter drink?
Vidya and Peter went for a picnic . Their mother gave them a water bottle that contained 5 liters of water. Vidya consumed 2/5 of the water. Peter consumed the remaining water. How much water did Vidya drink? How much water did Peter drink? - Building blocks
 Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each
Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each - A jug
 A jug holds 1 2/3 of a liter of water. How much does a 5 1/2 jug hold?
A jug holds 1 2/3 of a liter of water. How much does a 5 1/2 jug hold? - Tomato plant
 Bruce's grandmother loves to use fresh tomatoes in her homemade pasta sauce. Bruce thought she might like to grow her own, so he bought her a planter box and a tomato plant. The planter box is shaped like a rectangular prism. It is 12 1/2 inches long, 10
Bruce's grandmother loves to use fresh tomatoes in her homemade pasta sauce. Bruce thought she might like to grow her own, so he bought her a planter box and a tomato plant. The planter box is shaped like a rectangular prism. It is 12 1/2 inches long, 10 - Drain and inlet
 The reservoir is filled with inflow in 12 hours. It will drain through the drain in 9 hours. Can the tank overflow if we leave the inlet and outlet open at the same time?
The reservoir is filled with inflow in 12 hours. It will drain through the drain in 9 hours. Can the tank overflow if we leave the inlet and outlet open at the same time? - Ketchup vs mustard
 A 20-ounce bottle of ketchup costs $2.80. A 14-ounce bottle of mustard costs 2.38. Which item costs less per pound? How much less?
A 20-ounce bottle of ketchup costs $2.80. A 14-ounce bottle of mustard costs 2.38. Which item costs less per pound? How much less? - Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - Cesar
 Cesar increased the amount of water he drinks each day from 64 ounces to 72 ounces. By what percentage did Cesar increase the amount of water he drinks each day?
Cesar increased the amount of water he drinks each day from 64 ounces to 72 ounces. By what percentage did Cesar increase the amount of water he drinks each day? - The painter
 Alex had 5/6 liter of white paint. He used 1/8 of it to paint the walls and 2/5 of the remaining to paint the fence. How much paint is left?
Alex had 5/6 liter of white paint. He used 1/8 of it to paint the walls and 2/5 of the remaining to paint the fence. How much paint is left? - Solution mg/ml
 If 70 ml of solution contains 280mg of drug, how many milligrams of drugs are in 50 ml of solution?
If 70 ml of solution contains 280mg of drug, how many milligrams of drugs are in 50 ml of solution? - Complete 16
 Complete the conversions below, show calculations and answers 1) 3.5 kg to gram 2) 4567ml to litres 3) R45.78 to cent 4) 5.60m to centimeters
Complete the conversions below, show calculations and answers 1) 3.5 kg to gram 2) 4567ml to litres 3) R45.78 to cent 4) 5.60m to centimeters - A cube 3
 A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter?
A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter? - A two 2
 A two-wheeler covers 68.9 km in one liter of petrol. How much distance will it cover in 10 liters of petrol?
A two-wheeler covers 68.9 km in one liter of petrol. How much distance will it cover in 10 liters of petrol? - A frustum
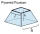 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Orange juice
 Water and orange are mixed in a ratio of 7:4. An amount of 36 cm³ of orange is used. What volume of water is used?
Water and orange are mixed in a ratio of 7:4. An amount of 36 cm³ of orange is used. What volume of water is used? - Smoothie 2
 David is using 100 ml of pineapple juice to make a smoothie. He needs to use a pineapple juice to orange juice ratio of 2: 5. How much orange juice should he use?
David is using 100 ml of pineapple juice to make a smoothie. He needs to use a pineapple juice to orange juice ratio of 2: 5. How much orange juice should he use? - 2-cycle
 2-cycle engines require a mixture of oil and gas to run properly. For every gallon of gas, a certain 2-cycle engine requires 1 1/4 fl oz of oil. How much oil must be added to prepare 3 1/2 gallons of gas to get the proper mixture?
2-cycle engines require a mixture of oil and gas to run properly. For every gallon of gas, a certain 2-cycle engine requires 1 1/4 fl oz of oil. How much oil must be added to prepare 3 1/2 gallons of gas to get the proper mixture? - Collin
 Collin is making fruit for a birthday party using the recipe below Ingredients Pink lemonade ; 1 1/2 gal Seltzer water ; 2 3/4 gal Fruit juice ; 7/8 gal Collin is using a punch bowl that holds 8 gallons of punch. How much more punch could Collin make the
Collin is making fruit for a birthday party using the recipe below Ingredients Pink lemonade ; 1 1/2 gal Seltzer water ; 2 3/4 gal Fruit juice ; 7/8 gal Collin is using a punch bowl that holds 8 gallons of punch. How much more punch could Collin make the
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
