Volume + square (second power, quadratic) - practice problems
Number of problems found: 514
- Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - A frustum
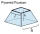 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid. - Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Calculate 83311
 The surface of the cuboid is S = 1714 cm². The edges are 25 and 14 cm long. Calculate its volume.
The surface of the cuboid is S = 1714 cm². The edges are 25 and 14 cm long. Calculate its volume. - Quadrilateral 83307
 The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism? - Cylinder's 83288
 Calculate the radius of the cylinder's base if its volume is equal to 12.56 cm².
Calculate the radius of the cylinder's base if its volume is equal to 12.56 cm². - Quadrilateral 83272
 Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm.
Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm. - Quadrilateral 83254
 What is the volume of a regular quadrilateral pyramid if its base edge a = √18 cm and side edge b = 5 cm?
What is the volume of a regular quadrilateral pyramid if its base edge a = √18 cm and side edge b = 5 cm? - Decimeters 83242
 The axial section of the cylinder is a square with a content of 56.25 cm². Calculate its surface area and volume. Express the result in square decimeters and cubic decimeters and round to hundredths.
The axial section of the cylinder is a square with a content of 56.25 cm². Calculate its surface area and volume. Express the result in square decimeters and cubic decimeters and round to hundredths. - Cylindrical 83193
 How much concrete is needed to pour 8 concrete columns with a square base: a = 38 cm, the height of the columns being 6.2 m? Each column has a cylindrical cavity with a diameter of 15 cm.
How much concrete is needed to pour 8 concrete columns with a square base: a = 38 cm, the height of the columns being 6.2 m? Each column has a cylindrical cavity with a diameter of 15 cm. - Original 83173
 When drying, the modeling mass loses 36% of its original volume. If the cube's volume is 5.12 dm³ after drying, what was the original length of the edge?
When drying, the modeling mass loses 36% of its original volume. If the cube's volume is 5.12 dm³ after drying, what was the original length of the edge? - Tetrahedron 83144
 A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise?
A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise? - Approximately 83106
 The castle courtyard, with an area of 100 m², is paved with oak cubes with an edge of 8 cm. Approximately 164 bricks were used to pave m². One dm³ of oak wood weighs 0.8 kg. Calculate the weight of all the bricks used to pave the courtyard.
The castle courtyard, with an area of 100 m², is paved with oak cubes with an edge of 8 cm. Approximately 164 bricks were used to pave m². One dm³ of oak wood weighs 0.8 kg. Calculate the weight of all the bricks used to pave the courtyard. - Calculate 83044
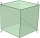 The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals.
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Centimeters 82996
 The volume of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Determine the height of the trapezoid in centimeters.
The volume of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Determine the height of the trapezoid in centimeters. - Calculate 82700
 A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume.
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Expression 82698
 Calculate the value of the expression V = 3x²- 2x + 3 for x = -2.
Calculate the value of the expression V = 3x²- 2x + 3 for x = -2. - Calculate 82690
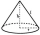 A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
