Harder math problems - last page
- Balls
 Three metal balls with volumes V1=81 cm³ V2=96 cm³ and V3=28 cm³ melted into one ball. Determine its surface area.
Three metal balls with volumes V1=81 cm³ V2=96 cm³ and V3=28 cm³ melted into one ball. Determine its surface area. - Plastic pipe
 Calculate the plastic pipe's weight with diameter d = 100 mm and length 330 cm if the wall thickness is 4 mm and the density of plastic is 1346 kg/m³.
Calculate the plastic pipe's weight with diameter d = 100 mm and length 330 cm if the wall thickness is 4 mm and the density of plastic is 1346 kg/m³. - Tiles
 From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have maximum 275 tiles.
From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have maximum 275 tiles. - Disco
 At the disco goes 12 boys and 15 girls. In how many ways can we select four dancing couples?
At the disco goes 12 boys and 15 girls. In how many ways can we select four dancing couples? - Boys and girls
 There are eight boys and nine girls in the class. There were six children on the trip from this class. What is the probability that: a) only boys went on the field trip b) just 2 boys went on the field trip
There are eight boys and nine girls in the class. There were six children on the trip from this class. What is the probability that: a) only boys went on the field trip b) just 2 boys went on the field trip - Cylinder
 Calculate the dimensions of rotating cylindrical containers with volume 2 l if the container's height equals the base's diameter.
Calculate the dimensions of rotating cylindrical containers with volume 2 l if the container's height equals the base's diameter. - Steeple
 We see the church tower from the road at an angle of 52°. When we zoom out to 29 meters away, it can be seen at an angle of 21°. How high is it?
We see the church tower from the road at an angle of 52°. When we zoom out to 29 meters away, it can be seen at an angle of 21°. How high is it? - Green - Red
 We have 5 bags. Each consists of one green and 2 red balls. From each, we pull just one ball. What is the probability that we don't pull any green ball?
We have 5 bags. Each consists of one green and 2 red balls. From each, we pull just one ball. What is the probability that we don't pull any green ball? - Diofant equation
 In the set of integers (Z), solve the equation: 212x +316y =0 Write result with integer parameter t in Z (parameter t = ...-2,-1,0,1,2,3... if equation has infinitely many solutions)
In the set of integers (Z), solve the equation: 212x +316y =0 Write result with integer parameter t in Z (parameter t = ...-2,-1,0,1,2,3... if equation has infinitely many solutions) - Gutter
 How much metal is needed to produce 60 pieces of gutter pipes with the diameter 17 cm and length of 6 m? The plate bends add 6% of the material.
How much metal is needed to produce 60 pieces of gutter pipes with the diameter 17 cm and length of 6 m? The plate bends add 6% of the material. - Heron backlaw
 Calculate the missing side in a triangle with sides 25 and 13 and area 152.
Calculate the missing side in a triangle with sides 25 and 13 and area 152. - Quadrilaterals 7224
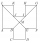 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode - Train
 The train is running at speeds of 96 km/h. From the beginning of braking to full stop, the train runs for 3.3 minutes. If the train slows the braking equally, calculate the distance from the location where you need to start to brake.
The train is running at speeds of 96 km/h. From the beginning of braking to full stop, the train runs for 3.3 minutes. If the train slows the braking equally, calculate the distance from the location where you need to start to brake. - Tangents
 To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center.
To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center. - Rhombus 2
 Calculate the rhombus area with a height v=48 mm and shorter diagonal u = 60 mm long.
Calculate the rhombus area with a height v=48 mm and shorter diagonal u = 60 mm long. - Steps
 How many steps do you save if you go square estate for diagonal (crosswise) rather than circumvent the two sides of its perimeter with 458 steps?
How many steps do you save if you go square estate for diagonal (crosswise) rather than circumvent the two sides of its perimeter with 458 steps? - N-gon II
 What is the side length of the regular 9-gon circumscribed circle of radius 13 cm?
What is the side length of the regular 9-gon circumscribed circle of radius 13 cm? - Circle in rhombus
 In the rhombus is an inscribed circle. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle area.
In the rhombus is an inscribed circle. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle area. - Cube - angles
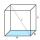 Calculate the angle between the wall diagonal and cube base. Calculate the angle between the cube body diagonal and the cube base.
Calculate the angle between the wall diagonal and cube base. Calculate the angle between the cube body diagonal and the cube base. - Diagonals of the rhombus
 Calculate the height of the rhombus whose diagonals are 18 cm and 6 cm.
Calculate the height of the rhombus whose diagonals are 18 cm and 6 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
