Equilateral triangle practice problems
See also practice problems: angle, triangle, right triangle, triangle inequality, similarity of triangles, The right triangle altitude theorem.We found these online calculators: conversion of volume units, triangle calculator.
Number of problems found: 0
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
For your searching, we found the following related math problems:
- Triangle KLB
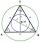 It is given equilateral triangle ABC. From point L, the midpoint of the side BC of the triangle, it is drawn perpendicular to the side AB. The intersection of the perpendicular and the side AB is point K. How many percents of the area of the triangle ABC
It is given equilateral triangle ABC. From point L, the midpoint of the side BC of the triangle, it is drawn perpendicular to the side AB. The intersection of the perpendicular and the side AB is point K. How many percents of the area of the triangle ABC - Equilateral cone
 We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Equilateral 4486
 If we increase one side of the triangle by 11 cm and reduce the other by 11 cm, we get an equilateral triangle. Four times the shortest side of the triangle is 10 cm greater than three times the triangle's longest side. Find all the lengths of the sides o
If we increase one side of the triangle by 11 cm and reduce the other by 11 cm, we get an equilateral triangle. Four times the shortest side of the triangle is 10 cm greater than three times the triangle's longest side. Find all the lengths of the sides o - Equilateral 6306
 We composed the diamond of four equilateral triangles with a side length of 7 cm. What's his circuit?
We composed the diamond of four equilateral triangles with a side length of 7 cm. What's his circuit? - Top of the tower
 The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join - Equilateral 75284
 Given are 6 line segments with lengths of 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm. How many equilateral triangles can make from them? List all the options.
Given are 6 line segments with lengths of 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm. How many equilateral triangles can make from them? List all the options. - Equilateral 83013
 Traffic signs are equilateral triangles with a side length of 900 mm. How many euros does a galvanized sheet cost to produce 50 pieces of such brands if we consider adding 15% of the material for waste? The price of 1 square meter of sheet metal is 6.5 eu
Traffic signs are equilateral triangles with a side length of 900 mm. How many euros does a galvanized sheet cost to produce 50 pieces of such brands if we consider adding 15% of the material for waste? The price of 1 square meter of sheet metal is 6.5 eu - Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Triangle
 Can an equilateral triangle have a right angle?
Can an equilateral triangle have a right angle? - Similarity coefficient
 The similarity ratio of two equilateral triangles is 4.3 (i.e., 43:10). The length of the side of the smaller triangle is 7.5 cm. Calculate the perimeter and area of the larger triangle.
The similarity ratio of two equilateral triangles is 4.3 (i.e., 43:10). The length of the side of the smaller triangle is 7.5 cm. Calculate the perimeter and area of the larger triangle. - Funnel
 The funnel has the shape of an equilateral cone. Calculate the surface wetted with water if we poured into the funnel 7.1 liters of water.
The funnel has the shape of an equilateral cone. Calculate the surface wetted with water if we poured into the funnel 7.1 liters of water. - EQL triangle
 Calculate the inradius and circumradius of an equilateral triangle with side a=77 cm.
Calculate the inradius and circumradius of an equilateral triangle with side a=77 cm. - Internal angles
 The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Triangle eq
 Calculate accurate to hundredths cm height of an equilateral triangle with a side length 12 cm. Calculate also its perimeter and area.
Calculate accurate to hundredths cm height of an equilateral triangle with a side length 12 cm. Calculate also its perimeter and area. - Equilateral 2543
 a) The perimeter of the equilateral triangle ABC is 63 cm. Calculate the side sizes of the triangle and its height. b) A right isosceles triangle has an area of 40.5 square meters. How big is his circuit? c) Calculate the square's area if the diagonal's s
a) The perimeter of the equilateral triangle ABC is 63 cm. Calculate the side sizes of the triangle and its height. b) A right isosceles triangle has an area of 40.5 square meters. How big is his circuit? c) Calculate the square's area if the diagonal's s - Equilateral 2714
 Determine the volume and surface of a 9 cm high triangular prism if the base is an equilateral triangle with a side of 8 cm.
Determine the volume and surface of a 9 cm high triangular prism if the base is an equilateral triangle with a side of 8 cm. - Prism - eq triangle
 Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm.
Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm. - Octahedron
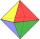 All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron.
All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron. - Candy - MO
 Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t
Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t - Equilateral 4301
 Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF?
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF?
