Dve tetivy 3
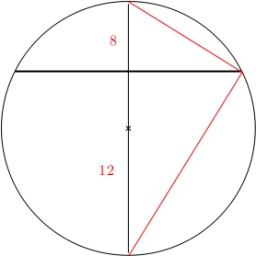
Vypočítajte dĺžku tetivy AB a k nej kolmej tetivy BC, ak tetiva AB je od stredu kružnice k vzdialená 4 cm a tetiva BC má vzdialenosť 8 cm.
Správna odpoveď:
Zobrazujem 3 komentáre:
Dr Math
mate pravdu, delku tetiv jsme popletli s x,y odvesnami v pravouhlom trojuhelniku, ktere jsou polovicne... Pak to vyjde spravne. Dekujeme!
4 roky 1 Like
Žiak
Stejná chyba jako v původním řešení, délka tětivy kružnice nemůže být větší než její průměr. Správně a = 16 cm, b = 8 cm, r = 4*sqrt 5 = cca 8,944 cm.
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Opísaná kružnica
 Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm.
Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm. - Kruh odsek/úsek
 Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku.
Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku. - V ubytovni
 V turistickej ubytovni spalo 44 žiakov v ôsmich izbách, niektoré boli štvorlôžkové, iné šiestich lôžkové, Koľko štvorlôžkových a kolík šiestich lôžkových izieb bolo v ubytovni, keď dve lôžka boli prázdne?
V turistickej ubytovni spalo 44 žiakov v ôsmich izbách, niektoré boli štvorlôžkové, iné šiestich lôžkové, Koľko štvorlôžkových a kolík šiestich lôžkových izieb bolo v ubytovni, keď dve lôžka boli prázdne? - Spravodlivo 4
 Vnučka Mia pomahala starkej 3 dní, Ema 2 dní a Zoja 4 dní. V akom pomerne ma starká rozdeliť čokoládu medzi vnučky, ak ich chce spravodlivo odmeniť podľa toho, ako dlho jej pomáhali.?
Vnučka Mia pomahala starkej 3 dní, Ema 2 dní a Zoja 4 dní. V akom pomerne ma starká rozdeliť čokoládu medzi vnučky, ak ich chce spravodlivo odmeniť podľa toho, ako dlho jej pomáhali.?
- Dĺžky 11
 Dĺžky hrán kvádra kvádra sú v pomere 1:2:3. Vypočítaj ich dĺžku, ak viete že povrch celého kvádra je S=5632 m². Vzkonajte skúšku správnosti výpočtu.
Dĺžky hrán kvádra kvádra sú v pomere 1:2:3. Vypočítaj ich dĺžku, ak viete že povrch celého kvádra je S=5632 m². Vzkonajte skúšku správnosti výpočtu. - Puk - hokej
 Hokejový brankár dostal za zápas 6 gólov. Úspešnosť jeho zákrokov bola 80%. Koľko striel chytil za zápas?
Hokejový brankár dostal za zápas 6 gólov. Úspešnosť jeho zákrokov bola 80%. Koľko striel chytil za zápas? - Žiaci 22
 Žiaci maturitného ročníka na OA v Banskej Bystrici mali z písomky zo slovenského jazyka nasledujúce známky: 2, 2, 3, 3, 1, 4, 4, 2, 3, 5, 3, 3, 3, 4, 2, 4, 1, 1,2,3,4,5,1, 3, 3, 2, 2, 3, 2, 1. Vytvorte tabuľku rozdelenia početnosti, určte čo je štatistick
Žiaci maturitného ročníka na OA v Banskej Bystrici mali z písomky zo slovenského jazyka nasledujúce známky: 2, 2, 3, 3, 1, 4, 4, 2, 3, 5, 3, 3, 3, 4, 2, 4, 1, 1,2,3,4,5,1, 3, 3, 2, 2, 3, 2, 1. Vytvorte tabuľku rozdelenia početnosti, určte čo je štatistick - Objem 41
 Objem pravidelného štvorbokého ihlanu je 72 cm³.Jeho výška sa rovná dĺžke podstavnej hrany. Vypočítaj dĺžku podstavnej a povrch ihlana.
Objem pravidelného štvorbokého ihlanu je 72 cm³.Jeho výška sa rovná dĺžke podstavnej hrany. Vypočítaj dĺžku podstavnej a povrch ihlana. - Povrch 31
 Povrch kvádra je S = 1714 cm / štvorcových/ Hrany majú dlžky 25 a 14 cm. Vypočítajte jeho objem.
Povrch kvádra je S = 1714 cm / štvorcových/ Hrany majú dlžky 25 a 14 cm. Vypočítajte jeho objem.
- Päť hostí
 Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba?
Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba? - Hrušiek 83295
 Cena 6 kg hrušiek je o 77 Kč vyššia ako cena 5 kg jabĺk. Cena 6 kg jabĺk je rovnaká ako cena 5 kg hrušiek. Koľko stojí 2 kg jabĺk?
Cena 6 kg hrušiek je o 77 Kč vyššia ako cena 5 kg jabĺk. Cena 6 kg jabĺk je rovnaká ako cena 5 kg hrušiek. Koľko stojí 2 kg jabĺk? - Výška, uhol a strana
 Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3. - Obvod 58
 Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby.
Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby. - Bočná hrana
 Aký je objem pravidelného štvorbokého ihlana, ak jeho podstavná hrana a = √18 cm a bočná hrana b = 5 cm?
Aký je objem pravidelného štvorbokého ihlana, ak jeho podstavná hrana a = √18 cm a bočná hrana b = 5 cm?
- Na výstave
 Na výstave bolo štyrikrát viac dievčat ako chlapcov. O koľko percent bolo na výstave viac dievčat ako chlapcov?
Na výstave bolo štyrikrát viac dievčat ako chlapcov. O koľko percent bolo na výstave viac dievčat ako chlapcov? - Rovnoramenný trojuholník -VU
 Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`.
Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`. - Jarka 3
 Jarka a Janka sa rozhodli vymaľovať si spoločnú izbu. Ak by ju maľovala Jarka sama, trvalo by jej to 4 hodiny. Janke by to trvalo 3 hodiny. Koľko by im trvalo vymaľovanie izby, ak by maľovali spolu?
Jarka a Janka sa rozhodli vymaľovať si spoločnú izbu. Ak by ju maľovala Jarka sama, trvalo by jej to 4 hodiny. Janke by to trvalo 3 hodiny. Koľko by im trvalo vymaľovanie izby, ak by maľovali spolu?
