Zrezaný kužeľ
Vypočítajte výšku rotačného zrezaného kužeľa, ak je daný jeho objem V = 802 cm3 a polomery podstáv r1 = 6 cm a r2 = 8 cm.
Správna odpoveď:
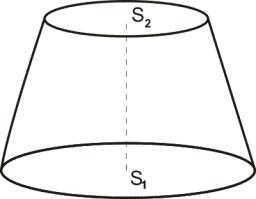
Tipy na súvisiace online kalkulačky
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Venuša
 Vypočítajte objem a povrch planéty Venuša, ak jej obvod je 12 000km.
Vypočítajte objem a povrch planéty Venuša, ak jej obvod je 12 000km. - Vypočítajte 74
 Vypočítajte hmotnosť dreveného pravidelného trojbokého hranola s výškou rovnajúcou sa obvodu podstavy a postavou vpísanou do kružnice s polomerom 6, M cm, kde M je mesiac vášho narodenia. Hustota duba je 680 kg/m³.
Vypočítajte hmotnosť dreveného pravidelného trojbokého hranola s výškou rovnajúcou sa obvodu podstavy a postavou vpísanou do kružnice s polomerom 6, M cm, kde M je mesiac vášho narodenia. Hustota duba je 680 kg/m³. - Radiátory
 Vypočítajte výkon radiátora, ak má tepelný spád (rozdiel teplôt vstupnej vody a spiatočky) a) 5°C b) 10°C c) 15°C d) 20°C a objemový prietok vykurovacej vody 45 kg/hod. Ako rýchlo prúdi voda v prívodnom potrubí k radiátoru e) DN16 a f) DN20? Označenie DN
Vypočítajte výkon radiátora, ak má tepelný spád (rozdiel teplôt vstupnej vody a spiatočky) a) 5°C b) 10°C c) 15°C d) 20°C a objemový prietok vykurovacej vody 45 kg/hod. Ako rýchlo prúdi voda v prívodnom potrubí k radiátoru e) DN16 a f) DN20? Označenie DN - Kruh odsek/úsek
 Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku.
Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku. - Koleso bicykla 5
 Aký priemer v centimetroch ma koleso bicykla, ak sa na dráhe dlhej 4082 m otočí 2000-krát
Aký priemer v centimetroch ma koleso bicykla, ak sa na dráhe dlhej 4082 m otočí 2000-krát - Dve podstavy
 Vypočítaj polomer podstavy valca, ak sa obsah jeho podstáv rovná 12,56 cm².
Vypočítaj polomer podstavy valca, ak sa obsah jeho podstáv rovná 12,56 cm². - Stĺp z tehál
 Stĺp vysoký 4m má tvar hranolu s postavou kosoštvorca s hranou dlhou 80cm a príslušnou výškou 70cm. Je postavený z tehál. Koľko tehál treba na jeho postavenie, ak jedna tehla ma objem 1,4 decimetre kubických?
Stĺp vysoký 4m má tvar hranolu s postavou kosoštvorca s hranou dlhou 80cm a príslušnou výškou 70cm. Je postavený z tehál. Koľko tehál treba na jeho postavenie, ak jedna tehla ma objem 1,4 decimetre kubických? - Kruh - obsah kruhu
 Vypočítaj obsah kruhu, ktorého polomer je 9 m. ( v metroch štvorcových )
Vypočítaj obsah kruhu, ktorého polomer je 9 m. ( v metroch štvorcových ) - Dve tetivy
 Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami.
Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami. - Tetiva - uhol
 Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm.
Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm. - Dve družnice
 Zostroj 2 kružnice tak aby ich stredy boli od seba vzdialene 5 cm a: a-nemali spoločný dotyk b- mali spoločný bod c-mali 2 spoločné body
Zostroj 2 kružnice tak aby ich stredy boli od seba vzdialene 5 cm a: a-nemali spoločný dotyk b- mali spoločný bod c-mali 2 spoločné body - Daný je 9
 Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice.
Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice. - Vypočítajte 257
 Vypočítajte súčet x-ových súradníc priesečníkov kružnice danej rovnicou (x - 1)²+ y² = 1 a priamky danej parametricky x = t, y = t , kde t∈R.
Vypočítajte súčet x-ových súradníc priesečníkov kružnice danej rovnicou (x - 1)²+ y² = 1 a priamky danej parametricky x = t, y = t , kde t∈R. - Na kruhovom 2
 Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2,5,9, čím vznikne trojuholník. Vypočítajte veľkosti všetkých vnútorných uhlov.
Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2,5,9, čím vznikne trojuholník. Vypočítajte veľkosti všetkých vnútorných uhlov. - Kužeľ a polkruh
 Ak je plášť kužeľa polkruh, potom priemer podstavy kužeľa je rovnaký ako dĺžka jeho strany. Dokážte.
Ak je plášť kužeľa polkruh, potom priemer podstavy kužeľa je rovnaký ako dĺžka jeho strany. Dokážte. - -2x-4y-20=0 82677
 Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0
Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0 - 2x+3y-4=0 82676
 Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0.
Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0.
