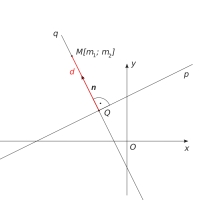
Parametrický tvar
Vypočítajte vzdialenosť bodu A [2,1] od priamky p:
X = -1 + 3t
Y = 5-4t
Priamka p má parametrický tvar rovnica priamky. ..
X = -1 + 3t
Y = 5-4t
Priamka p má parametrický tvar rovnica priamky. ..
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- analytická geometria
- vektor
- skalárny súčin
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- trojuholník
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Bod od roviny
 Vypočítaj vzdialenosť bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0
Vypočítaj vzdialenosť bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0 - Ako zistím
 Ako zistím uhlopriečky kosoštvorca, ak jeho obvod je 80dm a jedna uhlopriečka je 2x väčšia ako druhá?
Ako zistím uhlopriečky kosoštvorca, ak jeho obvod je 80dm a jedna uhlopriečka je 2x väčšia ako druhá? - Daný je 8
 Daný je rovnobežnik KLMN, v ktorom poznáme veľkosti strán/KL/ = a = 84,5 cm, /KN/ = 47,8 cm a veľkosť uhla pri vrchole K 56°40´. Vypočítajte veľkosť uhlopriečok.
Daný je rovnobežnik KLMN, v ktorom poznáme veľkosti strán/KL/ = a = 84,5 cm, /KN/ = 47,8 cm a veľkosť uhla pri vrchole K 56°40´. Vypočítajte veľkosť uhlopriečok. - 2x+3y-4=0 82676
 Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0.
Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0. - Vrcholy T3D
 Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A.
Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A. - Ohnisko a priamka
 Určte rovnicu paraboly, ktorá má bod F = [3,2] za svoje ohnisko a priamku x+y+1=0 za svoju radiacu priamku.
Určte rovnicu paraboly, ktorá má bod F = [3,2] za svoje ohnisko a priamku x+y+1=0 za svoju radiacu priamku. - Určte 19
 Určte rovnicu kružnice, ktorá je množinou všetkých bodov roviny, ktoré majú od bodu [3,7] dvakrát väčšiu vzdialenosť ako od bodu [0,1].
Určte rovnicu kružnice, ktorá je množinou všetkých bodov roviny, ktoré majú od bodu [3,7] dvakrát väčšiu vzdialenosť ako od bodu [0,1]. - Trojuholníka 82144
 Vypočítajte veľkosť výšky na stranu b (v_b) trojuholníka ABC s vrcholmi A[4;1;3] B[2;3;3] a C[1;1;3].
Vypočítajte veľkosť výšky na stranu b (v_b) trojuholníka ABC s vrcholmi A[4;1;3] B[2;3;3] a C[1;1;3]. - Matematika 2
 Do prepravného kontajnera s rozmermi a=10 m, b=4m, c=3m bola umiestnená drevená debna s rozmermi d=3m, e=4m a f=3m. Aká je maximálna dĺžka rovnej neohybnej tyče so zanedbateľným priemerom, ktorú je možné v tejto situácii ešte do kontejnera umiestniť?
Do prepravného kontajnera s rozmermi a=10 m, b=4m, c=3m bola umiestnená drevená debna s rozmermi d=3m, e=4m a f=3m. Aká je maximálna dĺžka rovnej neohybnej tyče so zanedbateľným priemerom, ktorú je možné v tejto situácii ešte do kontejnera umiestniť? - Aký vysoký
 Aký vysoký je strom keď oňho opriem rebrík dlhý 2 m. Rebrík je od stromu vzdialený 0,7 m a vrchná časť rebríka je opretá o strom v 2/3 jeho výšky?
Aký vysoký je strom keď oňho opriem rebrík dlhý 2 m. Rebrík je od stromu vzdialený 0,7 m a vrchná časť rebríka je opretá o strom v 2/3 jeho výšky? - Valeria
 Pani Clarkeová učí triedu 5. ročníka. Stojí 40 stôp pred Valeriou. Sarah sedí po Valeriinej pravici. Ak sú Sarah a pani Clarke vzdialené 50 stôp, ako ďaleko sú od seba Valeria a Sarah?
Pani Clarkeová učí triedu 5. ročníka. Stojí 40 stôp pred Valeriou. Sarah sedí po Valeriinej pravici. Ak sú Sarah a pani Clarke vzdialené 50 stôp, ako ďaleko sú od seba Valeria a Sarah? - Gotický
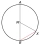
 Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice.
Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice. - Štvoruholník 13
 Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF.
Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF. - Tetiva 22
 Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku?
Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku? - Východiskového 80614
 Muž v púšti prejde 8,7 míle v smere S 26° W (juho-západ). Potom sa otočí o 90° a prejde 9 míľ v smere na N 49° W (severo západne). Ako ďaleko je v tom čase od svojho východiskového bodu a jeho postoj od jeho východiskového bodu?
Muž v púšti prejde 8,7 míle v smere S 26° W (juho-západ). Potom sa otočí o 90° a prejde 9 míľ v smere na N 49° W (severo západne). Ako ďaleko je v tom čase od svojho východiskového bodu a jeho postoj od jeho východiskového bodu? - Obvod trojuholníka 3
 Urči obvod trojuholníka ABC kde bod A je začiatok súradnicovej sústavy, bod B je priesečník grafu linearnej funkcie f: y = - 3/4• x + 3 s osou x a C je priesečník grafu tejto funkcie s osou y.
Urči obvod trojuholníka ABC kde bod A je začiatok súradnicovej sústavy, bod B je priesečník grafu linearnej funkcie f: y = - 3/4• x + 3 s osou x a C je priesečník grafu tejto funkcie s osou y. - Binibini
 Binibini vlastní trojuholníkový obytný pozemok ohraničený dvoma cestami, ktoré sa pretínajú v uhle 70°. Strany pozemku pozdĺž cesty sú 62 m a 43 m. Nájdite dĺžku plotu potrebnú na ohradenie pozemku. (vyjadrite odpovede s presnosťou na stotiny)
Binibini vlastní trojuholníkový obytný pozemok ohraničený dvoma cestami, ktoré sa pretínajú v uhle 70°. Strany pozemku pozdĺž cesty sú 62 m a 43 m. Nájdite dĺžku plotu potrebnú na ohradenie pozemku. (vyjadrite odpovede s presnosťou na stotiny)
