4-boký
Vypočítaj objem a povrch pravidelného štvorbokého ihlana, výška je 9 cm a dĺžka hrany základne 15 cm.
Správna odpoveď:

Zobrazujem 3 komentáre:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Chcete premeniť jednotku plochy?
Chcete premeniť jednotku dĺžky?
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Chcete premeniť jednotku plochy?
Chcete premeniť jednotku dĺžky?
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Povrch 31
 Povrch kvádra je S = 1714 cm / štvorcových/ Hrany majú dlžky 25 a 14 cm. Vypočítajte jeho objem.
Povrch kvádra je S = 1714 cm / štvorcových/ Hrany majú dlžky 25 a 14 cm. Vypočítajte jeho objem. - Obvod 58
 Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby.
Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby. - V kocke 2
 V kocke ABCDEFGH je obsah trojuholníka ABK √20cm². Koľko cm² má obsah útvaru ABGH v kocke ak vieš, že K je stred hrany CG?
V kocke ABCDEFGH je obsah trojuholníka ABK √20cm². Koľko cm² má obsah útvaru ABGH v kocke ak vieš, že K je stred hrany CG? - Vypočítajte 81939
 Povrch kvádra je 5 632 m². Dĺžky hrán sú v pomere 1 : 2 : 3. Vypočítajte objem kvádra.
Povrch kvádra je 5 632 m². Dĺžky hrán sú v pomere 1 : 2 : 3. Vypočítajte objem kvádra. - V našom
 V našom meste sa rozhodli zrekonštruovať kupolu hvezdárne a nanovo ju pokryť plechom. Minimálne koľko metrov štvorcových plechu budú potrebovať, ak kupola má tvar pologule s priemerom 6m
V našom meste sa rozhodli zrekonštruovať kupolu hvezdárne a nanovo ju pokryť plechom. Minimálne koľko metrov štvorcových plechu budú potrebovať, ak kupola má tvar pologule s priemerom 6m - Hrada
 Hrada má dĺžku 4 m a prierez tvaru štvorca, ktorého strana má dľžku 15 cm. Osem takýchto hrád treba natrieť farbou. Jedna kilogramová plechovka vystačí na 6 m² náteru. Koľko plechoviek farby treba kúpiť?
Hrada má dĺžku 4 m a prierez tvaru štvorca, ktorého strana má dľžku 15 cm. Osem takýchto hrád treba natrieť farbou. Jedna kilogramová plechovka vystačí na 6 m² náteru. Koľko plechoviek farby treba kúpiť? - Detský 7
 Detský bazén má tvar valca s priemerom podstavy 4 m a hĺbkou 50 cm (náčrt, výpočet, odpoveď). a) Vypočítaj objem vody v litroch, ktorý môže byť v bazéne, ak je naplnený po okraj. b) Ak bazén naplníme len na 75%, koľko litrov vody bude v bazéne? c) Ak chce
Detský bazén má tvar valca s priemerom podstavy 4 m a hĺbkou 50 cm (náčrt, výpočet, odpoveď). a) Vypočítaj objem vody v litroch, ktorý môže byť v bazéne, ak je naplnený po okraj. b) Ak bazén naplníme len na 75%, koľko litrov vody bude v bazéne? c) Ak chce - Pravidelného 80950
 Obvod podstavy pravidelného štvorbokého ihlana je rovnako veľký ako jeho výška. Ihlan má objem 288 dm³. Vypočítajte jeho povrch. Výsledok zaokrúhlite na celé dm².
Obvod podstavy pravidelného štvorbokého ihlana je rovnako veľký ako jeho výška. Ihlan má objem 288 dm³. Vypočítajte jeho povrch. Výsledok zaokrúhlite na celé dm². - Trojuholník skleník
 Skleník má tvar hranola položeného na bočnej stene. Podstavu tvorí lichobežník a trojuholník. Dolná základňa lichobežníka má dĺžku 3 m, horná základňa (a strana trojuholníka) má dĺžku 2 m, výška lichobežníka je 1,8 m a výška trojuholníka je 0,6 m. Výška h
Skleník má tvar hranola položeného na bočnej stene. Podstavu tvorí lichobežník a trojuholník. Dolná základňa lichobežníka má dĺžku 3 m, horná základňa (a strana trojuholníka) má dĺžku 2 m, výška lichobežníka je 1,8 m a výška trojuholníka je 0,6 m. Výška h - Vypočítajte 206
 Vypočítajte povrch a hranu kocky, ak jej objem sa rovná 3375 metrov kubických.
Vypočítajte povrch a hranu kocky, ak jej objem sa rovná 3375 metrov kubických. - Trojboký ihlan
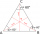
 Daný je kolmý pravidelný 3-boký ihlan. Strana podstavy a=5cm a výška je 8 cm. Vypočítaj objem a povrch.
Daný je kolmý pravidelný 3-boký ihlan. Strana podstavy a=5cm a výška je 8 cm. Vypočítaj objem a povrch. - Osovy 8
 Osovy rez kužeľa je rovnostranný trojuholník so stranou 12cm. Výpočet povrchu a objemu.
Osovy rez kužeľa je rovnostranný trojuholník so stranou 12cm. Výpočet povrchu a objemu. - Vypočítajte 203
 Vypočítajte hranu c a povrch S kvádra, ak jeho objem sa rovná 42 centimetrov kubických, a=6cm, b=3,5cm, c=?
Vypočítajte hranu c a povrch S kvádra, ak jeho objem sa rovná 42 centimetrov kubických, a=6cm, b=3,5cm, c=? - Strecha 16
 Strecha veže má tvar pravidelného 4-bokeho ihlana a výškou 4m a hranou podstavy 6m. Zistilo sa že je poškodených 25% krytiny na streche. Koľko metrov štvorcových krytiny treba na opravu strechy?
Strecha veže má tvar pravidelného 4-bokeho ihlana a výškou 4m a hranou podstavy 6m. Zistilo sa že je poškodených 25% krytiny na streche. Koľko metrov štvorcových krytiny treba na opravu strechy? - Maťko
 Maťko a Zuzka balia darčeky pre otca. Maťko má škatuľku v tvare kvádra s rozmermi 9cm, 3cm, 7cm a Zuzka škatuľku v tvare kocky s dlžkou hrany 3 cm. Koľko cm štvorcových baliaceho papiera minú spolu, ak na prekrývanie potrebujú 20% navyše?
Maťko a Zuzka balia darčeky pre otca. Maťko má škatuľku v tvare kvádra s rozmermi 9cm, 3cm, 7cm a Zuzka škatuľku v tvare kocky s dlžkou hrany 3 cm. Koľko cm štvorcových baliaceho papiera minú spolu, ak na prekrývanie potrebujú 20% navyše? - Vypočítajte 198
 Vypočítajte objem a povrch kužeľa, ktorého priemer podstavy je 6 cm a výška je 0,9 dm.
Vypočítajte objem a povrch kužeľa, ktorého priemer podstavy je 6 cm a výška je 0,9 dm. - Vypočítaj 349
 Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°.
Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°.
