Výška kruhového oblúka,vzorec
Vypočítajte výšku kruhového oblúka ak dĺžka oblúka je 77 a dĺžka tetivy 40.
Správna odpoveď:
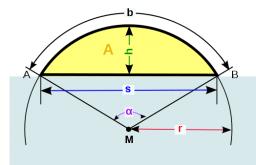
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Chcete premeniť jednotku dĺžky?
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Chcete premeniť jednotku dĺžky?
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- rovnica
- sústava rovníc
- vyjadrenie neznámej zo vzorca
- planimetria
- tetiva
- goniometria a trigonometria
- sínus
- kosínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Tri domy
 Tri domy tvoria trojuholníkový tvar. Dom A je 50 stôp od domu C a dom B je 60 stôp od domu C. Uhol ABC je 80 stupňov. Nakreslite obrázok a nájdite vzdialenosť medzi A a B.
Tri domy tvoria trojuholníkový tvar. Dom A je 50 stôp od domu C a dom B je 60 stôp od domu C. Uhol ABC je 80 stupňov. Nakreslite obrázok a nájdite vzdialenosť medzi A a B. - V rovnici
 V rovnici priamky p: ax-2y+1=0 určte koeficient a tak, aby priamka p: a) zvierala s kladným smerom osi x uhol 120°, b) prechádzala bodom A[3,-2], c) bola rovnobežná s osou x, d) mala smernicu k = 4.
V rovnici priamky p: ax-2y+1=0 určte koeficient a tak, aby priamka p: a) zvierala s kladným smerom osi x uhol 120°, b) prechádzala bodom A[3,-2], c) bola rovnobežná s osou x, d) mala smernicu k = 4. - V jednom 2
 V jednom trojuholníku je jeden uhol 43° a druhý je 15° menší ako tretí. Určte neznáme uhly trojuholníka.
V jednom trojuholníku je jeden uhol 43° a druhý je 15° menší ako tretí. Určte neznáme uhly trojuholníka. - Mnohouholnik 5
 V istom mnohouholniku platí, že pomer súčtu veľkosti jeho vnútorných uhlov a súčtu veľkosti k ním doplnkových uhlov je 2:5. Koľko vrcholov má tento mnohouholník?
V istom mnohouholniku platí, že pomer súčtu veľkosti jeho vnútorných uhlov a súčtu veľkosti k ním doplnkových uhlov je 2:5. Koľko vrcholov má tento mnohouholník?
- V štvoruholniku
 V štvoruholniku je uhol α dvakrát väčší od uhla β. uhol γ je 80% uhla α a uhol δ je o 30° väčší od uhla α. Urč uhly tohoto štvoruholnika.
V štvoruholniku je uhol α dvakrát väčší od uhla β. uhol γ je 80% uhla α a uhol δ je o 30° väčší od uhla α. Urč uhly tohoto štvoruholnika. - Tetiva 22
 Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku?
Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku? - Strom 21
 Strom, ktorý je na náprotivom brehu rieky vidíme pod uhlom 15° zo vzdialenosti 41m od brehu rieky. Z brehu rieky vidíme pod uhlom 31°. Aký vysoký je strom?
Strom, ktorý je na náprotivom brehu rieky vidíme pod uhlom 15° zo vzdialenosti 41m od brehu rieky. Z brehu rieky vidíme pod uhlom 31°. Aký vysoký je strom? - Vypočítajte 195
 Vypočítajte všetky vnútorné uhly v rovnoramennom trojuholníku ABC ak vieme, že BC je základňa a navyše vieme: |∢BAC|=α; |∢BCA|=4α
Vypočítajte všetky vnútorné uhly v rovnoramennom trojuholníku ABC ak vieme, že BC je základňa a navyše vieme: |∢BAC|=α; |∢BCA|=4α - V rovnobežníku 2
 V rovnobežníku je súčet dĺžok strán a+b = 234. Uhol zovretý stranami a a b je 60°. Dĺžka uhlopriečky proti danému uhlu 60° je u=162. Vypočítajte strany rovnobežníka, jeho obvod a obsah.
V rovnobežníku je súčet dĺžok strán a+b = 234. Uhol zovretý stranami a a b je 60°. Dĺžka uhlopriečky proti danému uhlu 60° je u=162. Vypočítajte strany rovnobežníka, jeho obvod a obsah.
- Pre súčet
 Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°?
Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°? - V trojuholníku 14
 V trojuholníku ABC urči veľkosť strán a a b a veľkosti vnútorných uhlov β a γ, ak je dané c = 1,86 m, tažnica na stranu c je 2,12 m a uhol alfa je 40° 12'.
V trojuholníku ABC urči veľkosť strán a a b a veľkosti vnútorných uhlov β a γ, ak je dané c = 1,86 m, tažnica na stranu c je 2,12 m a uhol alfa je 40° 12'. - Uhol BSA
 Je daná kružnica k (S; r) a bod A, ktorý leží na tejto kružnici. Na obvode leží aj bod B, pre ktorý platí, že je v jednom smere päťkrát ďalej od bodu A, než v opačnom smere (po obvode kružnice). Určte veľkosť konvexného uhla BSA.
Je daná kružnica k (S; r) a bod A, ktorý leží na tejto kružnici. Na obvode leží aj bod B, pre ktorý platí, že je v jednom smere päťkrát ďalej od bodu A, než v opačnom smere (po obvode kružnice). Určte veľkosť konvexného uhla BSA. - Uhol výseče
 Štvrťkruh s polomerom 4 má rovnaký obsah ako kruhový výsek o polomere 3. Aká je veľkosť stredového uhla výseče?
Štvrťkruh s polomerom 4 má rovnaký obsah ako kruhový výsek o polomere 3. Aká je veľkosť stredového uhla výseče? - Riešte GR
 Riešte goniometrickú rovnicu: cos(x-52°)=1
Riešte goniometrickú rovnicu: cos(x-52°)=1
- Súkolie
 Hnané koleso s polomerom 2 je spojené s hnacím kolesom s polomerom 1 remenicou s dĺžkou 17. Aká je vzdialenosť osí kolies?
Hnané koleso s polomerom 2 je spojené s hnacím kolesom s polomerom 1 remenicou s dĺžkou 17. Aká je vzdialenosť osí kolies? - Zrezaný 13
 Zrezaný rotačný kužeľ má podstavy s polomermi r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Aký je objem kužeľa, z ktorého zrezaný kužeľ vznikol?
Zrezaný rotačný kužeľ má podstavy s polomermi r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Aký je objem kužeľa, z ktorého zrezaný kužeľ vznikol? - MO Z7–I–6 2021
 V trojuholníku ABC leží na strane AC bod D a na strane BC bod E. Veľkosti uhlov ABD, BAE, CAE a CBD sú postupne 30°, 60°, 20° a 30°. určte veľkosť uhla AED.
V trojuholníku ABC leží na strane AC bod D a na strane BC bod E. Veľkosti uhlov ABD, BAE, CAE a CBD sú postupne 30°, 60°, 20° a 30°. určte veľkosť uhla AED.
