Narodeniny
V triede rozdávajú žiaci vždy o svojich narodeninách spolužiakom cukríky. Oslávenec dá vždy každému po jednom cukríka, sebe nedáva. Za rok sa v triede rozdalo celkom 650 cukríkov. Koľko žiakov je v triede? (Poznámka: Všetci žiaci triedy mali narodeniny v deň, keď sa konala výučba. )
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Puk - hokej
 Hokejový brankár dostal za zápas 6 gólov. Úspešnosť jeho zákrokov bola 80%. Koľko striel chytil za zápas?
Hokejový brankár dostal za zápas 6 gólov. Úspešnosť jeho zákrokov bola 80%. Koľko striel chytil za zápas? - Zrýchlenie 9
 Zrýchlenie hmotného bodu pri jeho priamočiarom pohybe rovnomerne klesá zo začiatočnej hodnoty a0 = 10 m/s² v čase t0 = 0 na nulovú hodnotu počas 20 s. Aká je rýchlosť hmotného bodu v čase t1 = 20 s a akú dráhu za ten čas hmotný bod prešiel, keď v čase t0
Zrýchlenie hmotného bodu pri jeho priamočiarom pohybe rovnomerne klesá zo začiatočnej hodnoty a0 = 10 m/s² v čase t0 = 0 na nulovú hodnotu počas 20 s. Aká je rýchlosť hmotného bodu v čase t1 = 20 s a akú dráhu za ten čas hmotný bod prešiel, keď v čase t0 - Hrušiek 83295
 Cena 6 kg hrušiek je o 77 Kč vyššia ako cena 5 kg jabĺk. Cena 6 kg jabĺk je rovnaká ako cena 5 kg hrušiek. Koľko stojí 2 kg jabĺk?
Cena 6 kg hrušiek je o 77 Kč vyššia ako cena 5 kg jabĺk. Cena 6 kg jabĺk je rovnaká ako cena 5 kg hrušiek. Koľko stojí 2 kg jabĺk? - Cukríky
 Jana a Klára si rozdelili cukríky v pomere 15 : 18. Klára dostala 90 cukríkov. Koľko bolo všetkých cukríkov?
Jana a Klára si rozdelili cukríky v pomere 15 : 18. Klára dostala 90 cukríkov. Koľko bolo všetkých cukríkov? - Jarka 3
 Jarka a Janka sa rozhodli vymaľovať si spoločnú izbu. Ak by ju maľovala Jarka sama, trvalo by jej to 4 hodiny. Janke by to trvalo 3 hodiny. Koľko by im trvalo vymaľovanie izby, ak by maľovali spolu?
Jarka a Janka sa rozhodli vymaľovať si spoločnú izbu. Ak by ju maľovala Jarka sama, trvalo by jej to 4 hodiny. Janke by to trvalo 3 hodiny. Koľko by im trvalo vymaľovanie izby, ak by maľovali spolu? - Nový hráč
 V družstve je 12 hráčov s priemernou výškou 185cm. Aká je výška nového hráča, ak sa po jeho príchode do družstva priemerná výška zvýšila o 1cm?
V družstve je 12 hráčov s priemernou výškou 185cm. Aká je výška nového hráča, ak sa po jeho príchode do družstva priemerná výška zvýšila o 1cm? - Anna malá
 Anna mala 3 krát viac ako Beátka. Cilka mala o 2 eura viac ako Beátka. Spolu mali 52 eur. Koľko mala každá?
Anna mala 3 krát viac ako Beátka. Cilka mala o 2 eura viac ako Beátka. Spolu mali 52 eur. Koľko mala každá? - Zamestnanci 4
 V sklade pracuje 21 zamestnancov - robotníkov a administratívnych pracovníkov. Pri úprave miezd znížili dennú odmenu každého administratívneho pracovníka o 3 € a dennú odmenu každého robotníka zvýšili o 2 €, takže celková denná mzda vzrástla o 17 €. Vypoč
V sklade pracuje 21 zamestnancov - robotníkov a administratívnych pracovníkov. Pri úprave miezd znížili dennú odmenu každého administratívneho pracovníka o 3 € a dennú odmenu každého robotníka zvýšili o 2 €, takže celková denná mzda vzrástla o 17 €. Vypoč - Tulipánov 83181
 Kyticu tvorí 13 narcisov, 8 tulipánov a ďalších 30% sú frézie, koľko kvetov je v kytici celkom?
Kyticu tvorí 13 narcisov, 8 tulipánov a ďalších 30% sú frézie, koľko kvetov je v kytici celkom? - Ak zmenšíme 3
 Ak zmenšíme dĺžku obdĺžnika o 2cm a šírku o 1cm, tak sa obsah obdĺžnika zmenší o 8 cm². Ak zväčšíme dĺžku obdĺžnika o 1cm a šírku o 2cm, tak sa obsah obdĺžnika zväčší o 13 cm². Aké boli pôvodné rozmery obdĺžnika?
Ak zmenšíme dĺžku obdĺžnika o 2cm a šírku o 1cm, tak sa obsah obdĺžnika zmenší o 8 cm². Ak zväčšíme dĺžku obdĺžnika o 1cm a šírku o 2cm, tak sa obsah obdĺžnika zväčší o 13 cm². Aké boli pôvodné rozmery obdĺžnika? - Učeň dostal
 Učeň dostal od majstra za úlohu rozdeliť elektrický kábel dĺžky 28m na dve časti tak, aby druhá časť bola 2,5 krát väčšia ako prvá časť. Ake dlhé mali byť časti kábla?
Učeň dostal od majstra za úlohu rozdeliť elektrický kábel dĺžky 28m na dve časti tak, aby druhá časť bola 2,5 krát väčšia ako prvá časť. Ake dlhé mali byť časti kábla? - Ťažnice v PT
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku. - Jednotky, dvojky, trojky
 V triede je 30 žiakov. Piati mali známku trojku. Ostatní dvojky a jednotky. Priemer známok bol 1,9. Koľko žiakov malo jednotku?
V triede je 30 žiakov. Piati mali známku trojku. Ostatní dvojky a jednotky. Priemer známok bol 1,9. Koľko žiakov malo jednotku? - Basketball
 V basketbalovej hre hodili hráči spolu 37 krát z toho boli za 2 body aj za 3 body spolu mali 82 bodov. Koľko bolo 2 bodových a koľko 3 bodových?
V basketbalovej hre hodili hráči spolu 37 krát z toho boli za 2 body aj za 3 body spolu mali 82 bodov. Koľko bolo 2 bodových a koľko 3 bodových? - Pokladník 4
 Pokladník Samuel mal v pokladni spolu 20 ks bankoviek v celkovej hodnote 850 eur. Boli to iba 50 eurové a 20 eurové bankovky. Koľko kusov mal z každej bankovky?
Pokladník Samuel mal v pokladni spolu 20 ks bankoviek v celkovej hodnote 850 eur. Boli to iba 50 eurové a 20 eurové bankovky. Koľko kusov mal z každej bankovky? - Test 22
 Irena řeší test. Během prvního čtení vyřešila tři čtvrtiny všech otázek, při kontrole pak ještě další šestinu. Dohromady tak vyřešila 22 otázek. Z kolika otázek se skládá celý test?
Irena řeší test. Během prvního čtení vyřešila tři čtvrtiny všech otázek, při kontrole pak ještě další šestinu. Dohromady tak vyřešila 22 otázek. Z kolika otázek se skládá celý test? - Trojuholníkov 83111
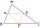 Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
