Dekanon
Vypočítajte obvod a obsah pravidelného 10 uholníka ak polomer opísanej kružnice r = 20 cm.
Správna odpoveď:
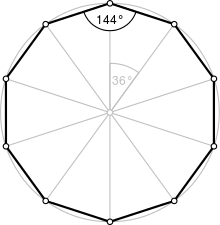
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- kruh, kružnica
- mnohouholník
- obsah
- obvod
- trojuholník
- goniometria a trigonometria
- sínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Trojuholník MO Z8-I-5
 Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD.
Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD. - Body ABC
 Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka?
Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka? - Mnohouholnik 5
 V istom mnohouholniku platí, že pomer súčtu veľkosti jeho vnútorných uhlov a súčtu veľkosti k ním doplnkových uhlov je 2:5. Koľko vrcholov má tento mnohouholník?
V istom mnohouholniku platí, že pomer súčtu veľkosti jeho vnútorných uhlov a súčtu veľkosti k ním doplnkových uhlov je 2:5. Koľko vrcholov má tento mnohouholník? - Určte 9
 Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine.
Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine. - Urč veľkosť
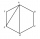 Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF.
Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF. - Zostrojte 11
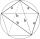 Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov
Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov - Štvoruholník ASBE
 Na obrázku je štvorec ABCD so stredom S a stranou dlhou 8 cm. Bod E je l'ubovoľný bod strany CD rozny od C a D. Vypočítajte obsah štvoruholníka ASBE v cm².
Na obrázku je štvorec ABCD so stredom S a stranou dlhou 8 cm. Bod E je l'ubovoľný bod strany CD rozny od C a D. Vypočítajte obsah štvoruholníka ASBE v cm². - Päťuholník 6
 Vývesný štít má tvar päťuholníka ABCDE, v ktorom úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je päta kolmice spustenie z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štíte je vyznačený bod X - priesečník úsečiek PE a
Vývesný štít má tvar päťuholníka ABCDE, v ktorom úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je päta kolmice spustenie z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štíte je vyznačený bod X - priesečník úsečiek PE a - Osemuholník oktagon
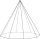 Potrebujeme zhotoviť podložku tvaru pravidelného osemuholníka o strane dĺžky 4cm. Aký minimálny priemer by mal mať polotovar tvaru kruhu, z ktorého máme podložku zhotoviť, a aký potom bude odpad v percentách? (Výsledky zaokrúhlite na 1 desatinné miesto)
Potrebujeme zhotoviť podložku tvaru pravidelného osemuholníka o strane dĺžky 4cm. Aký minimálny priemer by mal mať polotovar tvaru kruhu, z ktorého máme podložku zhotoviť, a aký potom bude odpad v percentách? (Výsledky zaokrúhlite na 1 desatinné miesto) - Oplotený
 Oplotený kvetinový záhon má tvar pravidelného šesťuholníka, vrcholy tvoria stĺpy plotu. Plot okolo záhona meria 60 m. K jednému zo stĺpikov je zvonka priviazaná koza, ktorá sa pasie na okolitej lúke (koza nemie vojsť do záhona). Špagát meria 24 m. Kolko m
Oplotený kvetinový záhon má tvar pravidelného šesťuholníka, vrcholy tvoria stĺpy plotu. Plot okolo záhona meria 60 m. K jednému zo stĺpikov je zvonka priviazaná koza, ktorá sa pasie na okolitej lúke (koza nemie vojsť do záhona). Špagát meria 24 m. Kolko m - Nepravidelný hexagon
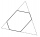 Je daný nepravidelný šesťuholník, ktorého strany sú rovnako dlhé. Protiľahlé strany sú rovnobežné a ich vzdialenosť je 237 resp. 195 resp. 193. Aká je jeho plocha?
Je daný nepravidelný šesťuholník, ktorého strany sú rovnako dlhé. Protiľahlé strany sú rovnobežné a ich vzdialenosť je 237 resp. 195 resp. 193. Aká je jeho plocha? - Pravidelného 46721
 Koľko litrov vody sa zmestí do ozdobnej záhradnej nádržky tvaru pravidelného šesťbokového ihlana s hranou podstavy dĺžky 30 cm? Hĺbka nádržky je 30 cm.
Koľko litrov vody sa zmestí do ozdobnej záhradnej nádržky tvaru pravidelného šesťbokového ihlana s hranou podstavy dĺžky 30 cm? Hĺbka nádržky je 30 cm. - Pravidelného 46451
 Vypočítajte povrch pravidelného štvorstenu, ak je dĺžka stenovej výšky Vs=1 dm
Vypočítajte povrch pravidelného štvorstenu, ak je dĺžka stenovej výšky Vs=1 dm - Na detskom 2
 Na detskom kolotoči v tvare kružnice je rovnomerne rozmiestnených 5 sedačiek. Aké dlhé je rameno kolotoča (spájajúce stred kolotoča so sedačkou), ak vzdialenosť medzi dvoma sedačkami je 1,2 m.
Na detskom kolotoči v tvare kružnice je rovnomerne rozmiestnených 5 sedačiek. Aké dlhé je rameno kolotoča (spájajúce stred kolotoča so sedačkou), ak vzdialenosť medzi dvoma sedačkami je 1,2 m. - Na detskom
 Na detskom kolotoči v tvare kružnice je rovnomerne rozmiestnených 12 sedačiek. Aké dlhé je rameno kolotoča (spájajúce stred kolotoča so sedačkou), ak vzdialenosť medzi dvoma sedačkami je 1,5m.
Na detskom kolotoči v tvare kružnice je rovnomerne rozmiestnených 12 sedačiek. Aké dlhé je rameno kolotoča (spájajúce stred kolotoča so sedačkou), ak vzdialenosť medzi dvoma sedačkami je 1,5m. - Pravidelného 44151
 Slnečník má tvar plášťa šesťibokého pravidelného ihlana, ktorého podstavná hrana a = 6dm a výška v = 25cm. Koľko látky je treba na zhotovenie slnečníka, ak počítame na spoje a odpad 10%.
Slnečník má tvar plášťa šesťibokého pravidelného ihlana, ktorého podstavná hrana a = 6dm a výška v = 25cm. Koľko látky je treba na zhotovenie slnečníka, ak počítame na spoje a odpad 10%. - Osemuholníka 43991
 Do kružnice je vpísaný nepravidelný konvexný osemuholník. Jeho 4 susediace strany majú dĺžku 3, zvyšné 4 susediace strany majú dĺžku 2. Aká je plocha daného osemuholníka?
Do kružnice je vpísaný nepravidelný konvexný osemuholník. Jeho 4 susediace strany majú dĺžku 3, zvyšné 4 susediace strany majú dĺžku 2. Aká je plocha daného osemuholníka?
