Katka MO
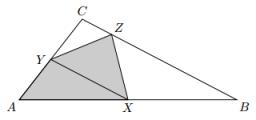
Katka narysovala trojuholník ABC. Stred strany AB si označila ako X a stred strany AC ako Y. Na strane BC chce nájsť taký bod Z, aby obsah štvoruholníka AXZY bol čo najväčší. Akú časť trojuholníka ABC môže maximálne zaberať štvoruholník AXZY?
Správna odpoveď:
Zobrazujem 2 komentáre:
Mo-1
Nápoveda. Určite, akú časť trojuholníka ABC zaberá trojuholník AXY.
Zo zadania vyplýva, že úsečka XY je strednou priečkou trojuholníka ABC, ktorá je rovnobežná so stranou BC. Jej dĺžka je teda polovičná vzhľadom k dĺžke strany BC a veľkosť výšky z A na XY je taktiež polovičná vzhľadom k veľkosti výšky z toho istého bodu na BC. To znamená, že trojuholník AXY má štvrtinový obsah vzhľadom na obsah trojuholníka ABC.
Teraz zvoľme bod Z na strane BC. Pretože úsečky BC a XY sú rovnobežné, je obsah trojuholníka XY Z, teda aj štvoruholníku XZY rovnaký pre akokoľvek zvolený bod Z. pretože vzdialenosť rovnobežiek BC a XY je rovnaká ako vzdialenosť XY od vrcholu A, majú trojuholníky AXY a XY Z tú istú veľkosť výšky na ich spoločnú stranu XY, a preto majú rovnaký obsah. Každý z týchto dvoch trojuholníkov zaberá štvrtinu trojuholníka ABC, štvoruholník AXZY preto zaberá polovicu trojuholníka ABC.
Zo zadania vyplýva, že úsečka XY je strednou priečkou trojuholníka ABC, ktorá je rovnobežná so stranou BC. Jej dĺžka je teda polovičná vzhľadom k dĺžke strany BC a veľkosť výšky z A na XY je taktiež polovičná vzhľadom k veľkosti výšky z toho istého bodu na BC. To znamená, že trojuholník AXY má štvrtinový obsah vzhľadom na obsah trojuholníka ABC.
Teraz zvoľme bod Z na strane BC. Pretože úsečky BC a XY sú rovnobežné, je obsah trojuholníka XY Z, teda aj štvoruholníku XZY rovnaký pre akokoľvek zvolený bod Z. pretože vzdialenosť rovnobežiek BC a XY je rovnaká ako vzdialenosť XY od vrcholu A, majú trojuholníky AXY a XY Z tú istú veľkosť výšky na ich spoločnú stranu XY, a preto majú rovnaký obsah. Každý z týchto dvoch trojuholníkov zaberá štvrtinu trojuholníka ABC, štvoruholník AXZY preto zaberá polovicu trojuholníka ABC.
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Zastroj
 Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie.
Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie. - Dve tetivy
 Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami.
Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami. - Dve družnice
 Zostroj 2 kružnice tak aby ich stredy boli od seba vzdialene 5 cm a: a-nemali spoločný dotyk b- mali spoločný bod c-mali 2 spoločné body
Zostroj 2 kružnice tak aby ich stredy boli od seba vzdialene 5 cm a: a-nemali spoločný dotyk b- mali spoločný bod c-mali 2 spoločné body - RST trojuholník
 Zisti, či je možné zostrojiť daný trojuholník a podľa, ktorej vety : RS = 2,5 cm ST = 7 cm TR = 4,5 cm
Zisti, či je možné zostrojiť daný trojuholník a podľa, ktorej vety : RS = 2,5 cm ST = 7 cm TR = 4,5 cm
- Zostroj 22
 Zostroj kosoštvorec, ktorý ma dĺžku strany 5 cm a výšku 4,5 cm. Náčrt: Rozbor: Konštrukcia: Postup:
Zostroj kosoštvorec, ktorý ma dĺžku strany 5 cm a výšku 4,5 cm. Náčrt: Rozbor: Konštrukcia: Postup: - Vo všeobecnom
 Vo všeobecnom lichobežníku VLAK platí: |VL| = 5,5cm; |VK| = 3,5cm; |LK| = 4,8cm; |
Vo všeobecnom lichobežníku VLAK platí: |VL| = 5,5cm; |VK| = 3,5cm; |LK| = 4,8cm; | - Priesečník uhlopriečok
 Zostroj rovnobežník ABCD, ak a=5 cm, Výška na stranu a je 5 cm a uhol ASB = 120 stupňov. S je priesečník uhlopriečok.
Zostroj rovnobežník ABCD, ak a=5 cm, Výška na stranu a je 5 cm a uhol ASB = 120 stupňov. S je priesečník uhlopriečok. - Zostroj 21
 Zostroj obdĺžnik ABCD ak a=8cm a dĺžka uhlopriečky AC je 13cm. Odmeraj dĺžku strán obdĺžnika.
Zostroj obdĺžnik ABCD ak a=8cm a dĺžka uhlopriečky AC je 13cm. Odmeraj dĺžku strán obdĺžnika. - Ostrouhlý trojuholník
 Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC.
Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC.
- Uhlopriečka 36
 Narysuj štvorec EFIJ, ak EI sa rovná 7cm.
Narysuj štvorec EFIJ, ak EI sa rovná 7cm. - Ťažnica a výška
 Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm
Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm - Strana výška a uhol
 Daná je úsečka BC dĺžky 6cm. Zostroj trojuholník tak, aby uhol BAC mal veľkosť 50°a výška na stranu a mala 5,5 cm. Ďakujem pekne.
Daná je úsečka BC dĺžky 6cm. Zostroj trojuholník tak, aby uhol BAC mal veľkosť 50°a výška na stranu a mala 5,5 cm. Ďakujem pekne. - Načrtnite 2
 Načrtnite sieť štvorbokého hranola, ktorého podstavou je obdĺžnik 1 cm x 3 cm a vysoký je 5 cm.
Načrtnite sieť štvorbokého hranola, ktorého podstavou je obdĺžnik 1 cm x 3 cm a vysoký je 5 cm. - ABCD(AB//CD): 70454
 Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60°
Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60°
- Zostroj 20
 Zostroj trojuholník HOP, ak o=6 cm, h=8cm a |PHO|=90°
Zostroj trojuholník HOP, ak o=6 cm, h=8cm a |PHO|=90° - Stredovo súmerný
 Koľko štvorčekov v sieti na obrázku treba ešte vymalovať, aby bol stredovo súmerný? štvorček - x x; o; o; x o; o; x; o x; o; o; o o; x; o; o toto je nakres štvorčekovej siete, kde vyfarbené štvorce sú x. Dakujem Lucia
Koľko štvorčekov v sieti na obrázku treba ešte vymalovať, aby bol stredovo súmerný? štvorček - x x; o; o; x o; o; x; o x; o; o; o o; x; o; o toto je nakres štvorčekovej siete, kde vyfarbené štvorce sú x. Dakujem Lucia - Zostrojte 11
 Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov
Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov
