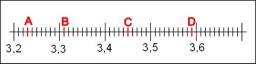
Číselná os
V kocúrskovskej škole používajú zvláštne číselnú os. Vzdialenosť medzi číslami 1 a 2 je 1 cm, vzdialenosť medzi číslami 2 a 3 je 3 cm, medzi číslami 3 a 4 je 5 cm, a tak ďalej, vzdialenosť medzi nasledujúce dvojicou prirodzenými číslami sa vždy zväčší o 2 cm.
Medzi ktorými dvoma prirodzenými číslami je na kocúrskovskej číselnej osi vzdialenosť 39 cm?
Nájdi všetky možnosti.
Medzi ktorými dvoma prirodzenými číslami je na kocúrskovskej číselnej osi vzdialenosť 39 cm?
Nájdi všetky možnosti.
Správna odpoveď:
Zobrazujem 1 komentár:
Mo-radca
Nápoveda. Vypíšte si vzdialenosti medzi rôznymi trojicami čísel na kocúrkovskej osi.
Možné riešenie.
Vzdialenosť 39 cm môže byť realizovaná medzi rôznymi dvojicami čísel. Budeme systematicky vypisovať vzdialenosti medzi niekoľkými prvými číslami kocúrkovskej osi. V nasledujúcej schéme je nad čiarou vypísané prvých 10 čísiel a pod čiarou skutočnej vzdialenosti (v cm) medzi rôznymi dvojicami týchto čísel - na prvom riadku pod čiarou sú postupne vzdialenosti medzi susednými číslami, na druhom riadku pod čiarou sú vzdialenosti medzi dvojicami čísel, ktoré sú ob jedno, atď. (Napr. 21 na treťom riadku pod čiarou značí skutočnú vzdialenosť medzi číslami 3 a 6 na kocúrkovskej osi a je určené ako 5 + 7 + 9). Hviezdičkou sú označené zbytočne veľké čísla, ktorá nás nezaujímajú.
1 2 3 4 5 6 7 8 9 10
1 3 5 7 9 11 13 15 17
4 8 12 16 20 24 28 32 36
9 15 21 27 33 39 * *
16 24 32 40 * * * *
25 35 45 * * * *
36 48 * * * * *
49 * * * * *
Ihneď vidíme (z tretieho riadku pod čiarou), že vzdialenosť 39 cm je medzi číslami 6 a 9 a že sa určite neobjavuje medzi číslami, ktoré sú na kocúrkovskej osi viac ako ob dve (od štvrtého riadku pod čiarou). Vzdialenosť 39 cm sa určite tiež nemôže objavovať medzi číslami, ktoré sú ob jedno, pretože všetky tieto vzdialenosti sú párne (druhý riadok pod čiarou). Zostáva teda preskúmať vzdialenosti medzi susednými číslami (prvý riadok pod čiarou):
Postupnosť vzdialenosťou medzi susednými číslami môžeme vyjadriť ako
1, 3 = 1 + 2, 5 = 1 + 2 · 2, 7 = 1 + 2 · 3, 9 = 1 + 2 · 4,. . .
Všeobecne, vzdialenosť medzi i-tím a (i + 1) -ným číslom na kocúrkovskej osi je rovná
1 + 2 (i - 1) = 2i - 1 (cm).
Táto vzdialenosť bude teda rovná 39 cm, práve keď i = 20. Vzdialenosť 39 cm na kocúrkovskej číselnej osi je medzi dvojicami čísel 6, 9 a 20, 21.
Poznámky.
a) Záverečnou úvahy možno nahradiť vypísaním a spočítaním všetkých nepárnych čísel až po 39. Ak je výpočet úplný, je takéto riešenie správne.
b) Naopak úvodnej vypisovanie možno celé nahradiť úvahou, príp. výpočtom: Všetky vzdialenosti v tabuľke sú súčtom rôznych počtov nepárnych čísel, pričom tieto počty sú buď nepárne (pre susedné čísla a dvojica čísel, ktoré sú ob párny počet čísel), alebo párne (pre dvojice čísel, ktoré sú ob nepárny počet čísiel). Na jednotlivých riadkoch sa teda objavujú buď len nepárne, alebo iba párne čísla. Vzdialenosť 39 cm sa teda môže objavovať iba medzi susednými číslami a dvojicami, ktoré sú na kocúrkovskej osi ob párny počet čísel.
Predchádzajúce vypisovanie postupnosti vzdialeností medzi susednými číslami má nasledujúce analógiu pre dvojice čísel, ktoré sú ob dve:
9, 15 = 9 + 6, 21 = 9 + 6 · 2, 27 = 9 + 6 · 3,. . .
Všeobecne, vzdialenosť medzi i-tím a (i + 3) -tým číslom na kocúrkovskej osi je rovná 9 + 6 (i - 1) = 6i + 3 (cm).
Táto vzdialenosť bude teda rovná 39 cm, práve keď i = 6. Obdobne možno vyjadriť akúkoľvek inú vyššie vypisovanie postupnosť.
c) Riešenie úlohy možno zjednodušiť pomocou nasledujúceho poznatku: Súčet nepárneho počtu po sebe idúcich nepárnych čísel je rovný súčinu počtu týchto čísel a prostredného z nich. Zvedavým riešiteľom odporúčame tento poznatok zdôvodniť a riešenie domyslieť.
d) V uvedenej schéme si môžeme všimnúť, že všetky čísla v prvom šikmom stĺpci sú druhými mocninami prirodzených čísel. To nie je náhoda - všeobecne platí, že súčet prvých k po sebe idúcich nepárnych čísel je rovný k2. Zvedavým riešiteľom odporúčame porovnať toto tvrdenie s poznatkom v predchádzajúcej poznámke.
Možné riešenie.
Vzdialenosť 39 cm môže byť realizovaná medzi rôznymi dvojicami čísel. Budeme systematicky vypisovať vzdialenosti medzi niekoľkými prvými číslami kocúrkovskej osi. V nasledujúcej schéme je nad čiarou vypísané prvých 10 čísiel a pod čiarou skutočnej vzdialenosti (v cm) medzi rôznymi dvojicami týchto čísel - na prvom riadku pod čiarou sú postupne vzdialenosti medzi susednými číslami, na druhom riadku pod čiarou sú vzdialenosti medzi dvojicami čísel, ktoré sú ob jedno, atď. (Napr. 21 na treťom riadku pod čiarou značí skutočnú vzdialenosť medzi číslami 3 a 6 na kocúrkovskej osi a je určené ako 5 + 7 + 9). Hviezdičkou sú označené zbytočne veľké čísla, ktorá nás nezaujímajú.
1 2 3 4 5 6 7 8 9 10
1 3 5 7 9 11 13 15 17
4 8 12 16 20 24 28 32 36
9 15 21 27 33 39 * *
16 24 32 40 * * * *
25 35 45 * * * *
36 48 * * * * *
49 * * * * *
Ihneď vidíme (z tretieho riadku pod čiarou), že vzdialenosť 39 cm je medzi číslami 6 a 9 a že sa určite neobjavuje medzi číslami, ktoré sú na kocúrkovskej osi viac ako ob dve (od štvrtého riadku pod čiarou). Vzdialenosť 39 cm sa určite tiež nemôže objavovať medzi číslami, ktoré sú ob jedno, pretože všetky tieto vzdialenosti sú párne (druhý riadok pod čiarou). Zostáva teda preskúmať vzdialenosti medzi susednými číslami (prvý riadok pod čiarou):
Postupnosť vzdialenosťou medzi susednými číslami môžeme vyjadriť ako
1, 3 = 1 + 2, 5 = 1 + 2 · 2, 7 = 1 + 2 · 3, 9 = 1 + 2 · 4,. . .
Všeobecne, vzdialenosť medzi i-tím a (i + 1) -ným číslom na kocúrkovskej osi je rovná
1 + 2 (i - 1) = 2i - 1 (cm).
Táto vzdialenosť bude teda rovná 39 cm, práve keď i = 20. Vzdialenosť 39 cm na kocúrkovskej číselnej osi je medzi dvojicami čísel 6, 9 a 20, 21.
Poznámky.
a) Záverečnou úvahy možno nahradiť vypísaním a spočítaním všetkých nepárnych čísel až po 39. Ak je výpočet úplný, je takéto riešenie správne.
b) Naopak úvodnej vypisovanie možno celé nahradiť úvahou, príp. výpočtom: Všetky vzdialenosti v tabuľke sú súčtom rôznych počtov nepárnych čísel, pričom tieto počty sú buď nepárne (pre susedné čísla a dvojica čísel, ktoré sú ob párny počet čísel), alebo párne (pre dvojice čísel, ktoré sú ob nepárny počet čísiel). Na jednotlivých riadkoch sa teda objavujú buď len nepárne, alebo iba párne čísla. Vzdialenosť 39 cm sa teda môže objavovať iba medzi susednými číslami a dvojicami, ktoré sú na kocúrkovskej osi ob párny počet čísel.
Predchádzajúce vypisovanie postupnosti vzdialeností medzi susednými číslami má nasledujúce analógiu pre dvojice čísel, ktoré sú ob dve:
9, 15 = 9 + 6, 21 = 9 + 6 · 2, 27 = 9 + 6 · 3,. . .
Všeobecne, vzdialenosť medzi i-tím a (i + 3) -tým číslom na kocúrkovskej osi je rovná 9 + 6 (i - 1) = 6i + 3 (cm).
Táto vzdialenosť bude teda rovná 39 cm, práve keď i = 6. Obdobne možno vyjadriť akúkoľvek inú vyššie vypisovanie postupnosť.
c) Riešenie úlohy možno zjednodušiť pomocou nasledujúceho poznatku: Súčet nepárneho počtu po sebe idúcich nepárnych čísel je rovný súčinu počtu týchto čísel a prostredného z nich. Zvedavým riešiteľom odporúčame tento poznatok zdôvodniť a riešenie domyslieť.
d) V uvedenej schéme si môžeme všimnúť, že všetky čísla v prvom šikmom stĺpci sú druhými mocninami prirodzených čísel. To nie je náhoda - všeobecne platí, že súčet prvých k po sebe idúcich nepárnych čísel je rovný k2. Zvedavým riešiteľom odporúčame porovnať toto tvrdenie s poznatkom v predchádzajúcej poznámke.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Hod kockou 2
 Päťkrát hodíme kockou . Napíš: a) 3 udalosti ktoré určite nemôžu nastať. Pri každej napíš dôvod. b) 3 udalosti ktoré určite nastanú pri každej napísať dôvod. A ďalšia úloha je 3 udalosti ktoré môžu ale nemusia nastať pri každej napísať dôvod.
Päťkrát hodíme kockou . Napíš: a) 3 udalosti ktoré určite nemôžu nastať. Pri každej napíš dôvod. b) 3 udalosti ktoré určite nastanú pri každej napísať dôvod. A ďalšia úloha je 3 udalosti ktoré môžu ale nemusia nastať pri každej napísať dôvod. - Liter 2
 Liter benzínu stojí 1,2€. Hmotnosť sa zvýšila po natankovani o 15kg. Hustota benzínu je p=750kg/m³ Za koľko eur som natankoval?
Liter benzínu stojí 1,2€. Hmotnosť sa zvýšila po natankovani o 15kg. Hustota benzínu je p=750kg/m³ Za koľko eur som natankoval? - Kosodĺžnik výšky
 Vypočítaj výšku kosodĺžnika ABCD na stranu BC, ak je AB=7cm, BC=5,5cm a výška prvej strany na AB=4,4cm
Vypočítaj výšku kosodĺžnika ABCD na stranu BC, ak je AB=7cm, BC=5,5cm a výška prvej strany na AB=4,4cm - Na číselnej osi 2
 Zobraz na číselnej osi všetky reálne čísla, ktoré sú väčšie, alebo sa rovnajú dvom a zároveň sú menšie ako 5.
Zobraz na číselnej osi všetky reálne čísla, ktoré sú väčšie, alebo sa rovnajú dvom a zároveň sú menšie ako 5. - Dažďová voda 2
 Aký objem musí mať nádrž v tvare valca aby sa v nej zachytila dažďová voda z plochej strechy domu v tvare kocky, keď je dom široký 12m a hlásia že spadne 50mm zrážok.
Aký objem musí mať nádrž v tvare valca aby sa v nej zachytila dažďová voda z plochej strechy domu v tvare kocky, keď je dom široký 12m a hlásia že spadne 50mm zrážok. - Presýpacie 2
 Presýpacie hodiny sa presypú trikrát za 5 minút. Koľkokrát sa presýpu za 2 hodiny?
Presýpacie hodiny sa presypú trikrát za 5 minút. Koľkokrát sa presýpu za 2 hodiny? - Cukríky
 Jana a Klára si rozdelili cukríky v pomere 15 : 18. Klára dostala 90 cukríkov. Koľko bolo všetkých cukríkov?
Jana a Klára si rozdelili cukríky v pomere 15 : 18. Klára dostala 90 cukríkov. Koľko bolo všetkých cukríkov? - Na mechanickú prácu
 Petra tlačila kreslo z jednej izby do druhej silou 60N. Vykonávala pri tom prácu 300 J .Ako ďaleko Petra kreslo odtlačila?
Petra tlačila kreslo z jednej izby do druhej silou 60N. Vykonávala pri tom prácu 300 J .Ako ďaleko Petra kreslo odtlačila? - Koleso bicykla 5
 Aký priemer v centimetroch ma koleso bicykla, ak sa na dráhe dlhej 4082 m otočí 2000-krát
Aký priemer v centimetroch ma koleso bicykla, ak sa na dráhe dlhej 4082 m otočí 2000-krát - Dve podstavy
 Vypočítaj polomer podstavy valca, ak sa obsah jeho podstáv rovná 12,56 cm².
Vypočítaj polomer podstavy valca, ak sa obsah jeho podstáv rovná 12,56 cm². - Katka
 Katka išla do nákupného centra pri jazere. Mala minúť 75 USD, kúpila si 3 položky, ktoré stáli 12,75 USD, 32,57 USD a 21,84 USD. Koľko ešte môže minúť?
Katka išla do nákupného centra pri jazere. Mala minúť 75 USD, kúpila si 3 položky, ktoré stáli 12,75 USD, 32,57 USD a 21,84 USD. Koľko ešte môže minúť? - Polievky
 Predávate polievkové zmesi pre charitu. Za každú polievkovú zmes, ktorú predáte, dostane spoločnosť, ktorá polievku vyrába, x dolárov a vy dostanete zvyšnú sumu. Predávate 16 polievkových zmesí spolu za (16x+96) dolárov. Koľko peňazí dostanete za každú po
Predávate polievkové zmesi pre charitu. Za každú polievkovú zmes, ktorú predáte, dostane spoločnosť, ktorá polievku vyrába, x dolárov a vy dostanete zvyšnú sumu. Predávate 16 polievkových zmesí spolu za (16x+96) dolárov. Koľko peňazí dostanete za každú po - Vypočítaj 448
 Vypočítaj povrch a objem pravidelného štvorbokého ihlana, ktorého hrana podstavy má dlžku 5 cm a ktorého výška je 10cm.
Vypočítaj povrch a objem pravidelného štvorbokého ihlana, ktorého hrana podstavy má dlžku 5 cm a ktorého výška je 10cm. - Polovica obĺžnika
 Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm.
Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm. - Mamička 6
 Mamička kúpila 6 lízaniek, za ktoré zaplatila 17 €. Najmenej koľko eur mohla stáť jedna lízanka, ak pokladníčka cenu nákupu zaokrúhlila na celé eurá?
Mamička kúpila 6 lízaniek, za ktoré zaplatila 17 €. Najmenej koľko eur mohla stáť jedna lízanka, ak pokladníčka cenu nákupu zaokrúhlila na celé eurá? - Obdĺžnikový 15
 Obdĺžnikový bazén má rozmery 25 metrov a 12,5 metra. Okolo bazéna je chodník široký 2 metre. Koľko metrov štvorcových dláždíc treba na vydláždenie chodníka?
Obdĺžnikový bazén má rozmery 25 metrov a 12,5 metra. Okolo bazéna je chodník široký 2 metre. Koľko metrov štvorcových dláždíc treba na vydláždenie chodníka? - Jednotková cena
 Keď stojí 5000g 120€, koľko bude stáť 100g?
Keď stojí 5000g 120€, koľko bude stáť 100g?
