Šesťuholník nepravidelný
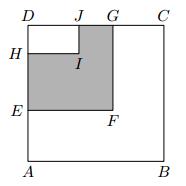
Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník EFGJIH má obvod 60 cm a obdĺžnik HIJD má obvod 28 cm. Určte obsah šesťuholníka EFGJIH.
Správna odpoveď:
Zobrazujem 1 komentár:
Mo-radce
Nápoveda. Dokážete určiť dĺžku niektoré úsečky, bez toho aby ste k tomu použili viac ako jeden zadaný rozmer?
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
8 rokov 1 Like
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Ťažnica a výška
 Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm
Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm - ABCD(AB//CD): 70454
 Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60°
Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60° - Rozdeľte 6
 Rozdeľte úsečku AB na tri rovnaké časti. Návod: Zostrojte rovnostranný trojuholník ABC a nájdite jeho stred (napr. Opísanej kružnice).
Rozdeľte úsečku AB na tri rovnaké časti. Návod: Zostrojte rovnostranný trojuholník ABC a nájdite jeho stred (napr. Opísanej kružnice). - Bod na priamke
 Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší.
Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší.
- Narysuj 9
 Narysuj úsečku AB=14 cm a rozdeľte ju pomocou redukčného uhla v pomere 2:9.
Narysuj úsečku AB=14 cm a rozdeľte ju pomocou redukčného uhla v pomere 2:9. - Stred kružnice
 Je daná ľubovolná kružnica k, ktorá nemá vyznačený stred. Pomocou vhodnej konštrukcie nájdi stred kružnice k. Vyskúšaj na 2 rôznych kružniciach.
Je daná ľubovolná kružnica k, ktorá nemá vyznačený stred. Pomocou vhodnej konštrukcie nájdi stred kružnice k. Vyskúšaj na 2 rôznych kružniciach. - Narysuj 8
 Narysuj lichobežník, ak b=4cm, c=7cm, d=4,5cm, v= 3 cm (Postup, diskusia, náčrt, rozbor, konštrukcia)
Narysuj lichobežník, ak b=4cm, c=7cm, d=4,5cm, v= 3 cm (Postup, diskusia, náčrt, rozbor, konštrukcia) - Ukážte 2
 Ukážte (pomocou Menealovej vety), že ťažisko delí ťažnicu v pomere 1:2.
Ukážte (pomocou Menealovej vety), že ťažisko delí ťažnicu v pomere 1:2. - ZIMA
 Mám pravouhlý lichobežník ZIMA (pravý uhol pri vrchole Z) ZI-7cm, ZM-5cm, AM-3,5cm a mám napísať aj postup a spraviť skúšku v konštrukčnej úlohe
Mám pravouhlý lichobežník ZIMA (pravý uhol pri vrchole Z) ZI-7cm, ZM-5cm, AM-3,5cm a mám napísať aj postup a spraviť skúšku v konštrukčnej úlohe
- C-I-2 2018 MO
 Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr
Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr - Kosodĺžnik 8
 Zostroj rovnobežník (kosodĺžnik) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm.
Zostroj rovnobežník (kosodĺžnik) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm. - Rovnakých 6890
 Úsečka MN (/MN/ = 9cm) rozdeľte na 11 rovnakých dielikov
Úsečka MN (/MN/ = 9cm) rozdeľte na 11 rovnakých dielikov - Narysuj 4
 Narýsuj úsečku KL=55mm. Narýsuj kružnicu k so stredom K a polomerom 4cm. Vyznačuj body tak, aby patrili kružnici a spájaj ich s bodom L.
Narýsuj úsečku KL=55mm. Narýsuj kružnicu k so stredom K a polomerom 4cm. Vyznačuj body tak, aby patrili kružnici a spájaj ich s bodom L. - Rovnoramenný lichobežník 9
 Narysuj rovnoramenný lichobežník ABDC, ak a=6cm, v=5cm, beta=60 stupňov. /náčrt, postup, konštrukcia/
Narysuj rovnoramenný lichobežník ABDC, ak a=6cm, v=5cm, beta=60 stupňov. /náčrt, postup, konštrukcia/
- Dorysuj 5456
 Dorysuj úsečku AB, ak poznáš jeden jej krajný bod a stred úsečky S.
Dorysuj úsečku AB, ak poznáš jeden jej krajný bod a stred úsečky S. - Kosoštvorec
 Skonštruujte kosoštvorec EFGH, kde e = 6,7cm, výška na stranu h: v = fh = 5cm
Skonštruujte kosoštvorec EFGH, kde e = 6,7cm, výška na stranu h: v = fh = 5cm - Kružnice 7
 Zostroj kružnice k1 (S1;r1) a k2(S2;r2), ak S1 S2 = 7 cm, d1= 12cm a r2 = 1/2 r1. Vyznač bod : a) A ležiaci na kružnici k1, b) B ležiaci v oboch kruhoch určených kružnicami k1 a k2, c) C ležiaci súčasne na oboch kružniciach, d) D, pre ktorý platí: (S1D)=
Zostroj kružnice k1 (S1;r1) a k2(S2;r2), ak S1 S2 = 7 cm, d1= 12cm a r2 = 1/2 r1. Vyznač bod : a) A ležiaci na kružnici k1, b) B ležiaci v oboch kruhoch určených kružnicami k1 a k2, c) C ležiaci súčasne na oboch kružniciach, d) D, pre ktorý platí: (S1D)=
