Do kužeľa
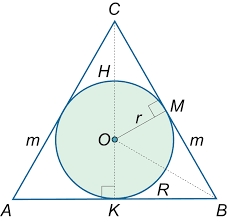
Do kužeľa je vpísaná guľa (prienik ich hraníc sa skladá z kružnice a jedného bodu). Pomer povrchu gule a obsahu podstavy je 4:3. Rovina, ktorá prechádza osou kužeľa, reže kužeľ v rovnoramennom trojuholníku. Určte veľkosť uhla oproti základni tohto trojuholníka.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Chcete premeniť jednotku plochy?
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Chcete premeniť jednotku plochy?
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- prienik množín
- stereometria
- kúžeľ
- guľa
- povrch telesa
- planimetria
- kruh, kružnica
- obsah
- trojuholník
- základné funkcie
- úmera, pomer
- goniometria a trigonometria
- tangens
- arkustangens
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Objem 40
 Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch.
Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch. - Daný je 7
 Daný je rovnoramenný lichobežník ABCD so základňami 10 cm a 14 cm. Výška lichobežníka je 6 cm. Určte vnútorné uhly lichobežníka.
Daný je rovnoramenný lichobežník ABCD so základňami 10 cm a 14 cm. Výška lichobežníka je 6 cm. Určte vnútorné uhly lichobežníka. - RR lichobežník
 Vypočítajte výšku v rovnoramennom lichobežníka, ak je obsah 520 cm² a základne a = 25 cm a c = 14cm. Vypočítajte vnútorné uhly lichobežníka.
Vypočítajte výšku v rovnoramennom lichobežníka, ak je obsah 520 cm² a základne a = 25 cm a c = 14cm. Vypočítajte vnútorné uhly lichobežníka. - Pozorovateľ 5
 Pozorovateľ leží na zemi vo vzdialenosti 20m od poľovníckeho posedu vysokého 5 m. A) Pod akým zorným uhlom vidí posed? B) O koľko sa zmení zorný uhol, ak sa k posedu priblíži o 5m?
Pozorovateľ leží na zemi vo vzdialenosti 20m od poľovníckeho posedu vysokého 5 m. A) Pod akým zorným uhlom vidí posed? B) O koľko sa zmení zorný uhol, ak sa k posedu priblíži o 5m? - Teleso, trenie
 Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou?
Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou? - Vypočítajte
 Vypočítajte veľkosť odchýlky telesové uhlopriečky a bočné hrany c kvádra s rozmermi: a = 28cm, b = 45cm a c = 73cm. Ďalej vypočítajte veľkosť odchýlky telesové uhlopriečkou od roviny podstavy.
Vypočítajte veľkosť odchýlky telesové uhlopriečky a bočné hrany c kvádra s rozmermi: a = 28cm, b = 45cm a c = 73cm. Ďalej vypočítajte veľkosť odchýlky telesové uhlopriečkou od roviny podstavy. - Pravidelný
 Pravidelný štvorboký ihlan má podstavnou hranu a = 1,56 dm a výšku v = 2,05dm. Vypočítajte: a) odchýlku roviny bočnej steny od roviny podstavy b) odchýlku bočnej hrany od roviny podstavy
Pravidelný štvorboký ihlan má podstavnou hranu a = 1,56 dm a výšku v = 2,05dm. Vypočítajte: a) odchýlku roviny bočnej steny od roviny podstavy b) odchýlku bočnej hrany od roviny podstavy - Dotyčnice a elipsa
 Nájdite veľkosť uhla, pod ktorým je elipsa x² + 5 y² = 5 viditeľná z bodu P [5, 1].
Nájdite veľkosť uhla, pod ktorým je elipsa x² + 5 y² = 5 viditeľná z bodu P [5, 1]. - Vzdialenosť bodov 2
 Je daný pravidelný štvorboký ihlan ABCDV, v ktorom AB= a= 4 cm a v= 8 cm. Nech S je stred CV. Vypočítajte vzdialenosť bodov A a S.
Je daný pravidelný štvorboký ihlan ABCDV, v ktorom AB= a= 4 cm a v= 8 cm. Nech S je stred CV. Vypočítajte vzdialenosť bodov A a S. - Na ceste 2
 Na ceste je značka pre stúpanie s uhlom 7%. Vypočítajte pod akým uhlom cesta stúpa ( klesá).
Na ceste je značka pre stúpanie s uhlom 7%. Vypočítajte pod akým uhlom cesta stúpa ( klesá). - Sever 2
 Vojenská jednotka pochoduje severným smerom z miesta A do miesta B vzdialeného 15 km. Z miesta B ide 12 km severovýchodným smerom do miesta C. Určite priamu vzdialenosť miest A, C a určite odchýlku -alfa- o ktorú sa jednotka odchýlila od severného smeru.
Vojenská jednotka pochoduje severným smerom z miesta A do miesta B vzdialeného 15 km. Z miesta B ide 12 km severovýchodným smerom do miesta C. Určite priamu vzdialenosť miest A, C a určite odchýlku -alfa- o ktorú sa jednotka odchýlila od severného smeru. - Šesťboký hranol uhly
 Daný je pravidelný šesťboký hranol ABCDEFGHIJKL, ktorý má všetky hrany rovnakej dĺžky. Zistite v stupňoch veľkosť uhla, ktorý zvierajú úsečky BK a CL.
Daný je pravidelný šesťboký hranol ABCDEFGHIJKL, ktorý má všetky hrany rovnakej dĺžky. Zistite v stupňoch veľkosť uhla, ktorý zvierajú úsečky BK a CL. - Špeh a opilec
 Po dlhom večeri vo vnútri salónika v tvare štvorca ABCD leží opitý kupec E tak, že trojuholník DEC je rovnostranný. Na hrane BC leží špeh F, pričom |EB|=|EF|. Aká je veľkosť uhla CEF?
Po dlhom večeri vo vnútri salónika v tvare štvorca ABCD leží opitý kupec E tak, že trojuholník DEC je rovnostranný. Na hrane BC leží špeh F, pričom |EB|=|EF|. Aká je veľkosť uhla CEF? - Zaokrúhli 7700
 Pod akým uhlom stúpa cesta, ak je stúpanie 8%? Zaokrúhli na desiatky minút.
Pod akým uhlom stúpa cesta, ak je stúpanie 8%? Zaokrúhli na desiatky minút. - Výška 9
 Výška pravidelného štvorbokého ihlanu je 6 cm, dĺžka strany podstavy je 4 cm. Aký uhol zvierajú strany ABV a BCV? ABCD je podstava, V vrchol.
Výška pravidelného štvorbokého ihlanu je 6 cm, dĺžka strany podstavy je 4 cm. Aký uhol zvierajú strany ABV a BCV? ABCD je podstava, V vrchol. - Výškový rozdiel 2
 Medzi strediskami je 15km a stúpanie je 13 promile. Aký je výškový rozdiel?
Medzi strediskami je 15km a stúpanie je 13 promile. Aký je výškový rozdiel? - Rovnoramenného 4589
 Pomer strán rovnoramenného trojuholníka je 7:6:7. Nájdite uhol na základni a zaokrúhlite ho na 3 platné číslice.
Pomer strán rovnoramenného trojuholníka je 7:6:7. Nájdite uhol na základni a zaokrúhlite ho na 3 platné číslice.
