Cesta okolo sveta
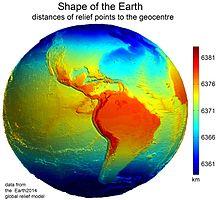
Akou priemernou rýchlosťou by ste sa museli pohybovať pri ceste okolo sveta za 80 dní? (Cestou po rovníku, uveďte zaokrúhlené na km / hod.)
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Chcete premeniť jednotku rýchlosti?
Chcete zaokrúhliť číslo?
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Chcete premeniť jednotku rýchlosti?
Chcete zaokrúhliť číslo?
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Vypočítajte 255
 Vypočítajte polomer železnej gule s hustotou 7,8g/cm3, hmotnosť je 7kg.
Vypočítajte polomer železnej gule s hustotou 7,8g/cm3, hmotnosť je 7kg. - V našom
 V našom meste sa rozhodli zrekonštruovať kupolu hvezdárne a nanovo ju pokryť plechom. Minimálne koľko metrov štvorcových plechu budú potrebovať, ak kupola má tvar pologule s priemerom 6m
V našom meste sa rozhodli zrekonštruovať kupolu hvezdárne a nanovo ju pokryť plechom. Minimálne koľko metrov štvorcových plechu budú potrebovať, ak kupola má tvar pologule s priemerom 6m - Koľko 156
 Koľko meria najkratšia vzdialenosť po povrchu glóbusu v mierke 1:1 000 000 z rovníka na severný pól?
Koľko meria najkratšia vzdialenosť po povrchu glóbusu v mierke 1:1 000 000 z rovníka na severný pól? - Dodržiavať 81618
 Koľko kopčekov zmrzliny urobíme pomocou naberačky v tvare guľového vrchlíka s polomerom 2,5 cm a výškou 4 cm. Máme k dispozícii vaničku zmrzliny s objemom 2 litre. Pri porciovaní budeme dodržiavať presnú mieru.
Koľko kopčekov zmrzliny urobíme pomocou naberačky v tvare guľového vrchlíka s polomerom 2,5 cm a výškou 4 cm. Máme k dispozícii vaničku zmrzliny s objemom 2 litre. Pri porciovaní budeme dodržiavať presnú mieru. - Vypočítaj 393
 Vypočítaj, koľko volejbalových lôpt s obvodom 65 cm sa zmestí do stojana tvaru kocky, ktorého hrana má dĺžku 100 cm.
Vypočítaj, koľko volejbalových lôpt s obvodom 65 cm sa zmestí do stojana tvaru kocky, ktorého hrana má dĺžku 100 cm. - Felix 2
 Vypočítajte akú časť Zeme Felix Baumgartner videl pri zoskoku z výšky 31 km. Polomer Zeme je R = 6378 km.
Vypočítajte akú časť Zeme Felix Baumgartner videl pri zoskoku z výšky 31 km. Polomer Zeme je R = 6378 km. - Guľa má
 Guľa má priemer 70 cm. Vypočítajte jej povrch a objem.
Guľa má priemer 70 cm. Vypočítajte jej povrch a objem. - Určte 10
 Určte objem guľovej vrstvy, ktorá vznikne z polgule s polomerom 5 cm odrezaním odseku, ktorého výška je 1,5 cm.
Určte objem guľovej vrstvy, ktorá vznikne z polgule s polomerom 5 cm odrezaním odseku, ktorého výška je 1,5 cm. - Povrch 29
 Povrch gule je 624 cm² . Vypočítajte jej polomer.
Povrch gule je 624 cm² . Vypočítajte jej polomer. - Guľová vrstva
 Aký je objem guľovej vrstvy, ktorá zostane po odrezaní odsekov z oboch strán gule, ktorých výška je 3,5 cm, Priemer gule je 24 cm.
Aký je objem guľovej vrstvy, ktorá zostane po odrezaní odsekov z oboch strán gule, ktorých výška je 3,5 cm, Priemer gule je 24 cm. - Do kocky 3
 Do kocky K s dĺžkou hrany a je vypísaná guľa G. Do gule G je vypísaná kocka K1. Vypočítaj, koľko percent objemu kocky K tvorí objem kocky K1.
Do kocky K s dĺžkou hrany a je vypísaná guľa G. Do gule G je vypísaná kocka K1. Vypočítaj, koľko percent objemu kocky K tvorí objem kocky K1. - Vypočítaj 327
 Vypočítaj povrch guľového odseku s výškou 6 cm a polomerom gule 15 cm
Vypočítaj povrch guľového odseku s výškou 6 cm a polomerom gule 15 cm - Priemer guľe
 Guľu s priemerom 10dm sme prerezali na dve rovnaké časti. Vypočítaj plochu rezu.
Guľu s priemerom 10dm sme prerezali na dve rovnaké časti. Vypočítaj plochu rezu. - Plynojem 4
 Plynojem tvorí valec vysoký 16m s priemerom 28m, ktorý je hore uzavretý guľovým vrchlíkom. Stred guľovej plochy leží 4m pod dnom valca. Vypočítate polomer guľovej plochy a výšku vrchlíka.
Plynojem tvorí valec vysoký 16m s priemerom 28m, ktorý je hore uzavretý guľovým vrchlíkom. Stred guľovej plochy leží 4m pod dnom valca. Vypočítate polomer guľovej plochy a výšku vrchlíka. - Venuša
 Vypočítajte objem a povrch planéty Venuša, ak jej obvod je 12 000km.
Vypočítajte objem a povrch planéty Venuša, ak jej obvod je 12 000km. - Bublina
 Vzduchová bublina na dne jazera v hĺbke h = 21 m má pri teplote t1 = 4°C polomer r1 = 1 cm. Bublina pomaly stúpa na povrch, pričom sa jej objem zväčšuje. Vypočítajte aký bude jej polomer, keď dosiahne povrch jazera, ktorý má teplotu t2 = 27°C. Atmosferick
Vzduchová bublina na dne jazera v hĺbke h = 21 m má pri teplote t1 = 4°C polomer r1 = 1 cm. Bublina pomaly stúpa na povrch, pričom sa jej objem zväčšuje. Vypočítajte aký bude jej polomer, keď dosiahne povrch jazera, ktorý má teplotu t2 = 27°C. Atmosferick - Pod guľou
 Kolmý kruhový kužeľ s hornou šírkou 24 cm a výškou 8 cm je naplnený vodou. V kuželi je ponorená guľová oceľová guľa s polomerom 3,0 cm. Nájdite objem vody pod guľou.
Kolmý kruhový kužeľ s hornou šírkou 24 cm a výškou 8 cm je naplnený vodou. V kuželi je ponorená guľová oceľová guľa s polomerom 3,0 cm. Nájdite objem vody pod guľou.
