Rebrík
4m rebrík sa dotýka kocky 1mx1m postavené pri stene. Ako vysoko na stene dosiahne?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- V 50
 V 50 litrovej nádobe je 45 litrov vody. Koľko litrov vody v nej bude, ak do nej dolejeme ešte 10 litrov vody?
V 50 litrovej nádobe je 45 litrov vody. Koľko litrov vody v nej bude, ak do nej dolejeme ešte 10 litrov vody? - Spotreba
 Spotreba benzínu na kilometer M (jednotka kilometer na liter) auta Dodge Caliber je modelovaná funkciou M(s) = - 1/28s² + 3s- 31 Akú má auto najlepšiu spotrebu (benzínové kilometre) a akú rýchlosť dosiahne?
Spotreba benzínu na kilometer M (jednotka kilometer na liter) auta Dodge Caliber je modelovaná funkciou M(s) = - 1/28s² + 3s- 31 Akú má auto najlepšiu spotrebu (benzínové kilometre) a akú rýchlosť dosiahne? - V triedach
 V triedach zoskupených udajov, ako sú 10-15, 16-20, 21-25, 26-30 s príslušnými frekvenciami každej triedy ako 3, 5, 4, 3, potom rozsah (variacné rozpätie) je: a. 15 b. 6 c. 20 d. 5
V triedach zoskupených udajov, ako sú 10-15, 16-20, 21-25, 26-30 s príslušnými frekvenciami každej triedy ako 3, 5, 4, 3, potom rozsah (variacné rozpätie) je: a. 15 b. 6 c. 20 d. 5 - Rodina 8
 Rodina Nováková si zobrala z banky úver (pôžičku) 120 000 eur. Aká bola výška poplatku za spracovanie, zriadenie a poskytnutie úveru, ak podľa sadzobníka poplatkov banky je jeho výška 0,80percent z objemu úveru, minimálne však 250eur a maximálne 950eur?
Rodina Nováková si zobrala z banky úver (pôžičku) 120 000 eur. Aká bola výška poplatku za spracovanie, zriadenie a poskytnutie úveru, ak podľa sadzobníka poplatkov banky je jeho výška 0,80percent z objemu úveru, minimálne však 250eur a maximálne 950eur? - Poistenie
 James má poistenie ochrany pred zranením, ktorá kryje liečebné náklady pre každú osobu v jeho aute, na ňom, okolo neho alebo pod ním. Každá osoba môže získať až 50 000 dolárov. James je účastníkom nehody a traja ľudia sú zranení. Jedna osoba má liečebné n
James má poistenie ochrany pred zranením, ktorá kryje liečebné náklady pre každú osobu v jeho aute, na ňom, okolo neho alebo pod ním. Každá osoba môže získať až 50 000 dolárov. James je účastníkom nehody a traja ľudia sú zranení. Jedna osoba má liečebné n - Zo železnej
 Zo železnej tyče v tvare hranola s rozmermi 5,6 cm 4,8 cm, 7,2 cm je potrebné vyrobiť čo najväčšiu kužeľ. a) Vypočítajte jeho objem. b) Vypočítajte odpad.
Zo železnej tyče v tvare hranola s rozmermi 5,6 cm 4,8 cm, 7,2 cm je potrebné vyrobiť čo najväčšiu kužeľ. a) Vypočítajte jeho objem. b) Vypočítajte odpad. - Ivan a
 Ivan a Katka objavili na dovolenke pravidelný ihlan, ktorého podstavou bol štvorec so stranou 230 m a ktorého výška bola rovná polomeru kruhu s rovnakým obsahom ako podstavný štvorec. Katka označila vrcholy štvorca ABCD. Ivan vyznačil na priamke spájajúce
Ivan a Katka objavili na dovolenke pravidelný ihlan, ktorého podstavou bol štvorec so stranou 230 m a ktorého výška bola rovná polomeru kruhu s rovnakým obsahom ako podstavný štvorec. Katka označila vrcholy štvorca ABCD. Ivan vyznačil na priamke spájajúce - Bod na priamke
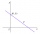 Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší.
Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší. - Drevený 3
 Drevený kváder má rozmery 12 cm, 24 cm a 30 cm. Peter ho chce rozrezať na niekoľko zhodných kociek. Najmenej koľko kociek môže dostať?
Drevený kváder má rozmery 12 cm, 24 cm a 30 cm. Peter ho chce rozrezať na niekoľko zhodných kociek. Najmenej koľko kociek môže dostať? - Ktorý 2
 Ktorý kosoštvorec so stranou dlhou 7,5 cm má: a/najväčší obsah, b/najmenší obsah
Ktorý kosoštvorec so stranou dlhou 7,5 cm má: a/najväčší obsah, b/najmenší obsah - 352/5000
Strelec
 352/5000 Strelec strieľa do terča, pričom predpokladáme, že jednotlivé výstrely sú navzájom nezávislé a pravdepodobnosť zásahu je u každého z nich 0,2. Strelec strieľa tak dlho, kým prvýkrát terč nezasiahne, potom streľbu ukončí. (A) Aký je najpravdepodob
352/5000 Strelec strieľa do terča, pričom predpokladáme, že jednotlivé výstrely sú navzájom nezávislé a pravdepodobnosť zásahu je u každého z nich 0,2. Strelec strieľa tak dlho, kým prvýkrát terč nezasiahne, potom streľbu ukončí. (A) Aký je najpravdepodob - Derivačný príklad
 Súčet dvoch čísel je 12. Nájdite tieto čísla, ak: a) Súčet ich tretích mocnín je minimálna. b) Súčin jedného s treťou mocninou druhého je maximálna. c) Obe sú kladné a súčin jedného s druhou mocninou druhého je maximálna.
Súčet dvoch čísel je 12. Nájdite tieto čísla, ak: a) Súčet ich tretích mocnín je minimálna. b) Súčin jedného s treťou mocninou druhého je maximálna. c) Obe sú kladné a súčin jedného s druhou mocninou druhého je maximálna. - Simplexová metóda
 Reťazec obchodných domov plánuje investovať do televíznej reklamy až 24 000 Eur. Všetky reklamné spoty budú umiestnené na televíznej stanici, na ktorej odvysielanie 30 sekundového spotu stojí 1000 Eur a sleduje ho 14 000 potenciálnych zákazníkov, počas pr
Reťazec obchodných domov plánuje investovať do televíznej reklamy až 24 000 Eur. Všetky reklamné spoty budú umiestnené na televíznej stanici, na ktorej odvysielanie 30 sekundového spotu stojí 1000 Eur a sleduje ho 14 000 potenciálnych zákazníkov, počas pr - Číslo 110
 Číslo 110 chceme rozdeliť na 3 sčítance tak, aby prvý a druhý boli v pomere 4 : 5 a tretí s prvým v pomere 7 : 3. Vypočítajte najmenší zo sčítancov.
Číslo 110 chceme rozdeliť na 3 sčítance tak, aby prvý a druhý boli v pomere 4 : 5 a tretí s prvým v pomere 7 : 3. Vypočítajte najmenší zo sčítancov. - Lavičkách 18013
 V parku je 12 lavičiek. Na lavičku sa môžu posadiť 4 osoby. Na každej z nich sedia najmenej 2 osoby. Koľko najmenej a najviac osôb sedí na lavičkách?
V parku je 12 lavičiek. Na lavičku sa môžu posadiť 4 osoby. Na každej z nich sedia najmenej 2 osoby. Koľko najmenej a najviac osôb sedí na lavičkách? - Kvíz 4
 V súťaži odpovedá 10 súťažiacich na päť otázok, v každom kole na jednu otázku. Kto odpovie správne, získa v danom kole toľko bodov, koľko súťažiacich odpovedalo nesprávne. Jedna zo súťažiacich po súťaži povedala : Celkovo sme získali 116 bodov, z toho ja
V súťaži odpovedá 10 súťažiacich na päť otázok, v každom kole na jednu otázku. Kto odpovie správne, získa v danom kole toľko bodov, koľko súťažiacich odpovedalo nesprávne. Jedna zo súťažiacich po súťaži povedala : Celkovo sme získali 116 bodov, z toho ja - Poklad
 Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad.
Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad.
