MO-Z6-I-2 2017
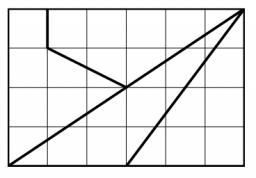
Erika chcela ponúknuť čokoládu svojim trom kamarátkam. Keď ju vytiahla z batohu, zistila, že je polámaná ako na obrázku. (Vyznačené štvorčeky sú navzájom zhodné. ) Dievčatá sa dohodli, že čokoládu ďalej lámať nebudú a lósom určia, aký veľký kúsok ktorá dostane. Zoraďte štyri kúsky čokolády odnajmenšieho po najväčší.
Správna odpoveď:
Zobrazujem 5 komentárov:
Dr Math
S1 = je obsah trojuholnika vpravo dole, zakladna 3 , vyska 4....
S2 = je obsah trojuholnika vlavo dole, opat zakladna 3 a vyska 4...
S3 je obsah 4 uholnika vpravo hore co vyzera takmer ako trojuholnik. Sklada sa z odcitnia obsahov dvoch trojuholnikov.
a) trojuholnika o zakladni 7 a vysky 2. Zakladna 7 (obdlznik ma dlhsiu stranu len 6) preto lebo predlzenie ciary smerujuce vlavo hore pretne predlzenu stranu obdlznika, tak ze zformuje trojuholnik o zakladni 7.... tj. o jeden dielik vlavo od horneho laveho vrcholu obdlznika. Inymi slovami ciara smerujuca vlavo hore, iduca v sklone 1 dielik vertikalne ku 2 horizontalne pretne predlzenu stranu obdlznika az 1 dielik od vrcholu.
b) a musime odcitat obsah pravouhleho trojuholnika o odvesne 1 a druhej odvesne 2.
S4 je obsah obdlznika minus S1+S2+S3 (zvysna plocha)
S2 = je obsah trojuholnika vlavo dole, opat zakladna 3 a vyska 4...
S3 je obsah 4 uholnika vpravo hore co vyzera takmer ako trojuholnik. Sklada sa z odcitnia obsahov dvoch trojuholnikov.
a) trojuholnika o zakladni 7 a vysky 2. Zakladna 7 (obdlznik ma dlhsiu stranu len 6) preto lebo predlzenie ciary smerujuce vlavo hore pretne predlzenu stranu obdlznika, tak ze zformuje trojuholnik o zakladni 7.... tj. o jeden dielik vlavo od horneho laveho vrcholu obdlznika. Inymi slovami ciara smerujuca vlavo hore, iduca v sklone 1 dielik vertikalne ku 2 horizontalne pretne predlzenu stranu obdlznika az 1 dielik od vrcholu.
b) a musime odcitat obsah pravouhleho trojuholnika o odvesne 1 a druhej odvesne 2.
S4 je obsah obdlznika minus S1+S2+S3 (zvysna plocha)
6 rokov 3 Likes
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Odpočítajú 82333
 Myslím si tri čísla, keď ich sčítam dostanem 16, keď od súčtu prvých dvoch čísel odpočítajú tretie dostanem 10, keď od súčtu prvého a tretieho čísla odčítajú druhé dostanem 8. Ktoré čísla si myslím?
Myslím si tri čísla, keď ich sčítam dostanem 16, keď od súčtu prvých dvoch čísel odpočítajú tretie dostanem 10, keď od súčtu prvého a tretieho čísla odčítajú druhé dostanem 8. Ktoré čísla si myslím? - Nikola
 Nikola mala v zošite napísané jedno trojciferne a jedno dvojciferné číslo. Každé z týchto čísel bolo tvorené navzájom rôznymi číslicami. Rozdiel Nikolinych čísel bol 976. Aký bol ich súčet?
Nikola mala v zošite napísané jedno trojciferne a jedno dvojciferné číslo. Každé z týchto čísel bolo tvorené navzájom rôznymi číslicami. Rozdiel Nikolinych čísel bol 976. Aký bol ich súčet? - Z6–I–5 MO 2019
 Útvar na obrázku vznikol tak, že z veľkého kríža bol vystrihnutý malý kríž. Každý z týchto krížov môže byť zložený z piatich zhodných štvorcov, pričom strany malých štvorcov sú polovičné vzhľadom na strany veľkých štvorcov. Obsah sivého útvaru je 45 cm².
Útvar na obrázku vznikol tak, že z veľkého kríža bol vystrihnutý malý kríž. Každý z týchto krížov môže byť zložený z piatich zhodných štvorcov, pričom strany malých štvorcov sú polovičné vzhľadom na strany veľkých štvorcov. Obsah sivého útvaru je 45 cm². - MO Z7–I–3 2019
 Roman má rád kúzla a matematiku. Naposledy čaroval s trojcifernými alebo štvorcifernými číslami takto: • z daného čísla vytvoril dve pomocné čísla tak, že ho rozdelil medzi ciframi na mieste stoviek a desiatok (napr. Z čísla 581 by dostal 5 a 81), • pomoc
Roman má rád kúzla a matematiku. Naposledy čaroval s trojcifernými alebo štvorcifernými číslami takto: • z daného čísla vytvoril dve pomocné čísla tak, že ho rozdelil medzi ciframi na mieste stoviek a desiatok (napr. Z čísla 581 by dostal 5 a 81), • pomoc
- Z5 – I – 5
 Tomáš dostal deväť kartičiek, na ktorých boli nasledujúce čísla a matematické symboly matematická olympiáda výsledky. 18, 19, 20, 20, +, -, x, (, ) Pozn. 4 čísla a operátory plus, mínus, krát, ľavá zátvorka, pravá zátvorka. Kartičky ukladal tak, že vedľa
Tomáš dostal deväť kartičiek, na ktorých boli nasledujúce čísla a matematické symboly matematická olympiáda výsledky. 18, 19, 20, 20, +, -, x, (, ) Pozn. 4 čísla a operátory plus, mínus, krát, ľavá zátvorka, pravá zátvorka. Kartičky ukladal tak, že vedľa - MO Z6–I–1 - 2017 - Anička
 Anička a Blanka si napísali každá jedno dvojciferné číslo, ktoré začínalo sedmičkou. Dievčatá si zvolili rôzne čísla. Potom každá medzi obe cifry vložila nulu, takže im vzniklo trojciferné číslo. Od neho každá odčítala svoje pôvodné dvojciferné číslo. Výs
Anička a Blanka si napísali každá jedno dvojciferné číslo, ktoré začínalo sedmičkou. Dievčatá si zvolili rôzne čísla. Potom každá medzi obe cifry vložila nulu, takže im vzniklo trojciferné číslo. Od neho každá odčítala svoje pôvodné dvojciferné číslo. Výs - Utierky
 Mamička vyprala štvorcové utierky a vešia je vedľa seba na šnúru natiahnutú medzi dvoma stromami. Použila šnúru s dĺžkou 7,5 metra, pričom na uviazanie okolo kmeňa potrebovala na každej strane 8 dm. Všetky utierky majú šírku 45 cm. Medzi krajné utierky a
Mamička vyprala štvorcové utierky a vešia je vedľa seba na šnúru natiahnutú medzi dvoma stromami. Použila šnúru s dĺžkou 7,5 metra, pričom na uviazanie okolo kmeňa potrebovala na každej strane 8 dm. Všetky utierky majú šírku 45 cm. Medzi krajné utierky a - Katka
 Katka išla do nákupného centra pri jazere. Mala minúť 75 USD, kúpila si 3 položky, ktoré stáli 12,75 USD, 32,57 USD a 21,84 USD. Koľko ešte môže minúť?
Katka išla do nákupného centra pri jazere. Mala minúť 75 USD, kúpila si 3 položky, ktoré stáli 12,75 USD, 32,57 USD a 21,84 USD. Koľko ešte môže minúť? - Prienik či zjednotenie
 V triede je 24 žiakov. psa má doma 11 z nich. Drobného hlodavca má 15 z nich. Žiadne zvieratko nemá doma 5 žiakov. Koľko žiakov má doma 2 zvieratká?
V triede je 24 žiakov. psa má doma 11 z nich. Drobného hlodavca má 15 z nich. Žiadne zvieratko nemá doma 5 žiakov. Koľko žiakov má doma 2 zvieratká?
- Peter
 Peter kúpil 58 nohavíc a 18 nohavíc sa roztrhlo. Koľko nemal roztrhnutých nohavíc, ktoré mal?
Peter kúpil 58 nohavíc a 18 nohavíc sa roztrhlo. Koľko nemal roztrhnutých nohavíc, ktoré mal? - Súčin - produkt
 O koľko je súčin 2½ a 3⅘ menší ako 20?
O koľko je súčin 2½ a 3⅘ menší ako 20? - Z drevenej 2
 Z drevenej plátne tvár obdĺžnika s rozmermi 80 CM a 65 CM odrezal stolár pravoúhly trojuholník s voľnými stranami 550 mm a 200 mm. kolko centimetrov štvorcových bude tvoriť odpad?
Z drevenej plátne tvár obdĺžnika s rozmermi 80 CM a 65 CM odrezal stolár pravoúhly trojuholník s voľnými stranami 550 mm a 200 mm. kolko centimetrov štvorcových bude tvoriť odpad? - V záhrade 5
 V záhrade rozkvitlo 43 tulipánov. Mama natrhala do vázy 21 tulipánov. Koľko tulipánov zostalo kvitnúť v záhrade?
V záhrade rozkvitlo 43 tulipánov. Mama natrhala do vázy 21 tulipánov. Koľko tulipánov zostalo kvitnúť v záhrade? - Trojuholníkov 83111
 Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
- Kríky
 Mason vždy pomáha orezávať kríky. Plocha A mala dĺžku 14 m a šírku 7 m a ak ideme dokopy A a B, rovná sa 215 m². Otázka znie: aká je plocha B?
Mason vždy pomáha orezávať kríky. Plocha A mala dĺžku 14 m a šírku 7 m a ak ideme dokopy A a B, rovná sa 215 m². Otázka znie: aká je plocha B? - Aká suma
 Aká suma mi vyjde, keď zo sumy 30000, ak odrátam 1/8 z nej?
Aká suma mi vyjde, keď zo sumy 30000, ak odrátam 1/8 z nej? - Priklad – 8. rocnik (asi MO)
 Adam napı́sal nasledujúci súčet s piatimi tajnými sčı́tancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré na
Adam napı́sal nasledujúci súčet s piatimi tajnými sčı́tancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré na
