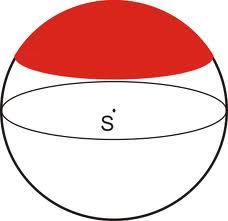
Guľový odsek
Z guľe s polomerom 27 bol odrezaný guľový odsek. Jehu výška je 16. Akú časť objemu gule tvorí objem odseku?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- rovnica
- stereometria
- guľa
- guľový vrchlík
- planimetria
- Pytagorova veta
- základné funkcie
- percentá
- čísla
- reálne čísla
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Vypočítajte 255
 Vypočítajte polomer železnej gule s hustotou 7,8g/cm3, hmotnosť je 7kg.
Vypočítajte polomer železnej gule s hustotou 7,8g/cm3, hmotnosť je 7kg. - V našom
 V našom meste sa rozhodli zrekonštruovať kupolu hvezdárne a nanovo ju pokryť plechom. Minimálne koľko metrov štvorcových plechu budú potrebovať, ak kupola má tvar pologule s priemerom 6m
V našom meste sa rozhodli zrekonštruovať kupolu hvezdárne a nanovo ju pokryť plechom. Minimálne koľko metrov štvorcových plechu budú potrebovať, ak kupola má tvar pologule s priemerom 6m - Koľko 156
 Koľko meria najkratšia vzdialenosť po povrchu glóbusu v mierke 1:1 000 000 z rovníka na severný pól?
Koľko meria najkratšia vzdialenosť po povrchu glóbusu v mierke 1:1 000 000 z rovníka na severný pól? - Dodržiavať 81618
 Koľko kopčekov zmrzliny urobíme pomocou naberačky v tvare guľového vrchlíka s polomerom 2,5 cm a výškou 4 cm. Máme k dispozícii vaničku zmrzliny s objemom 2 litre. Pri porciovaní budeme dodržiavať presnú mieru.
Koľko kopčekov zmrzliny urobíme pomocou naberačky v tvare guľového vrchlíka s polomerom 2,5 cm a výškou 4 cm. Máme k dispozícii vaničku zmrzliny s objemom 2 litre. Pri porciovaní budeme dodržiavať presnú mieru.
- Vypočítaj 393
 Vypočítaj, koľko volejbalových lôpt s obvodom 65 cm sa zmestí do stojana tvaru kocky, ktorého hrana má dĺžku 100 cm.
Vypočítaj, koľko volejbalových lôpt s obvodom 65 cm sa zmestí do stojana tvaru kocky, ktorého hrana má dĺžku 100 cm. - Felix 2
 Vypočítajte akú časť Zeme Felix Baumgartner videl pri zoskoku z výšky 31 km. Polomer Zeme je R = 6378 km.
Vypočítajte akú časť Zeme Felix Baumgartner videl pri zoskoku z výšky 31 km. Polomer Zeme je R = 6378 km. - Guľa má
 Guľa má priemer 70 cm. Vypočítajte jej povrch a objem.
Guľa má priemer 70 cm. Vypočítajte jej povrch a objem. - Určte 10
 Určte objem guľovej vrstvy, ktorá vznikne z polgule s polomerom 5 cm odrezaním odseku, ktorého výška je 1,5 cm.
Určte objem guľovej vrstvy, ktorá vznikne z polgule s polomerom 5 cm odrezaním odseku, ktorého výška je 1,5 cm. - Povrch 29
 Povrch gule je 624 cm² . Vypočítajte jej polomer.
Povrch gule je 624 cm² . Vypočítajte jej polomer.
- Guľová vrstva
 Aký je objem guľovej vrstvy, ktorá zostane po odrezaní odsekov z oboch strán gule, ktorých výška je 3,5 cm, Priemer gule je 24 cm.
Aký je objem guľovej vrstvy, ktorá zostane po odrezaní odsekov z oboch strán gule, ktorých výška je 3,5 cm, Priemer gule je 24 cm. - Do kocky 3
 Do kocky K s dĺžkou hrany a je vypísaná guľa G. Do gule G je vypísaná kocka K1. Vypočítaj, koľko percent objemu kocky K tvorí objem kocky K1.
Do kocky K s dĺžkou hrany a je vypísaná guľa G. Do gule G je vypísaná kocka K1. Vypočítaj, koľko percent objemu kocky K tvorí objem kocky K1. - Vypočítaj 327
 Vypočítaj povrch guľového odseku s výškou 6 cm a polomerom gule 15 cm
Vypočítaj povrch guľového odseku s výškou 6 cm a polomerom gule 15 cm - Priemer guľe
 Guľu s priemerom 10dm sme prerezali na dve rovnaké časti. Vypočítaj plochu rezu.
Guľu s priemerom 10dm sme prerezali na dve rovnaké časti. Vypočítaj plochu rezu. - Plynojem 4
 Plynojem tvorí valec vysoký 16m s priemerom 28m, ktorý je hore uzavretý guľovým vrchlíkom. Stred guľovej plochy leží 4m pod dnom valca. Vypočítate polomer guľovej plochy a výšku vrchlíka.
Plynojem tvorí valec vysoký 16m s priemerom 28m, ktorý je hore uzavretý guľovým vrchlíkom. Stred guľovej plochy leží 4m pod dnom valca. Vypočítate polomer guľovej plochy a výšku vrchlíka.
- Venuša
 Vypočítajte objem a povrch planéty Venuša, ak jej obvod je 12 000km.
Vypočítajte objem a povrch planéty Venuša, ak jej obvod je 12 000km. - Bublina
 Vzduchová bublina na dne jazera v hĺbke h = 21 m má pri teplote t1 = 4°C polomer r1 = 1 cm. Bublina pomaly stúpa na povrch, pričom sa jej objem zväčšuje. Vypočítajte aký bude jej polomer, keď dosiahne povrch jazera, ktorý má teplotu t2 = 27°C. Atmosferick
Vzduchová bublina na dne jazera v hĺbke h = 21 m má pri teplote t1 = 4°C polomer r1 = 1 cm. Bublina pomaly stúpa na povrch, pričom sa jej objem zväčšuje. Vypočítajte aký bude jej polomer, keď dosiahne povrch jazera, ktorý má teplotu t2 = 27°C. Atmosferick - Pod guľou
 Kolmý kruhový kužeľ s hornou šírkou 24 cm a výškou 8 cm je naplnený vodou. V kuželi je ponorená guľová oceľová guľa s polomerom 3,0 cm. Nájdite objem vody pod guľou.
Kolmý kruhový kužeľ s hornou šírkou 24 cm a výškou 8 cm je naplnený vodou. V kuželi je ponorená guľová oceľová guľa s polomerom 3,0 cm. Nájdite objem vody pod guľou.
