Sklon úsečky
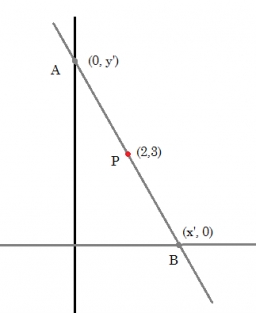
Úsečka má svoje koncové body na súradnicových osiach a formuje s nimi trojuholník s plochou 36 štvorcových jednotiek. Úsečka prechádza bodom (5,2). Aký je sklon úsečky?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- analytická geometria
- priamka
- úsečka
- algebra
- kvadratická rovnica
- vyjadrenie neznámej zo vzorca
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- obsah
- trojuholník
- čísla
- zlomky
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Mimobežky
 Je daný kváder ABCDEFGH. Vieme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítajte v stupňoch veľkosť uhla, ktorý zvierajú priamky BG a FH .
Je daný kváder ABCDEFGH. Vieme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítajte v stupňoch veľkosť uhla, ktorý zvierajú priamky BG a FH . - Parametrické 33451
 Priamka p je daná bodom P [ - 0,5;1] a smerovým vektorom s= (1,5; - 3) určite: A) hodnotu parametra t pre body X [- 1,5;3], Y [1; - 2] priamky p B) či body R [0,5; - 1], S [1,5;3] leží na priamke p C) parametrické rovnice priamky m || p, ak prechádza pria
Priamka p je daná bodom P [ - 0,5;1] a smerovým vektorom s= (1,5; - 3) určite: A) hodnotu parametra t pre body X [- 1,5;3], Y [1; - 2] priamky p B) či body R [0,5; - 1], S [1,5;3] leží na priamke p C) parametrické rovnice priamky m || p, ak prechádza pria - Parametrické rovnice
 Sú dané body A(1,2), B(4,-2) a C(3,-2) . Nájdite parametrické rovnice priamky, ktorá: a) Prechádza bodom C a je rovnobežná s priamkou AB, b) Prechádza bodom C a je kolmá k priamke AB.
Sú dané body A(1,2), B(4,-2) a C(3,-2) . Nájdite parametrické rovnice priamky, ktorá: a) Prechádza bodom C a je rovnobežná s priamkou AB, b) Prechádza bodom C a je kolmá k priamke AB. - Priamky
 Nájdite hodnotu t, ak priamky 2tx + 5y-6 = 0 a 5x-4y + 8 = 0 sú kolmé, rovnobežné. Aký uhol zviera každá z priamok s osou x, nájdite uhol medzi čiarami?
Nájdite hodnotu t, ak priamky 2tx + 5y-6 = 0 a 5x-4y + 8 = 0 sú kolmé, rovnobežné. Aký uhol zviera každá z priamok s osou x, nájdite uhol medzi čiarami? - Uhol priamky a roviny
 Určte uhol priamky, ktorá je určená parametricky x=5+t y=1+3t z=-2t t patri R a roviny, ktorá je určená všeobecnou rovnicou 2x-y+3z-4=0.
Určte uhol priamky, ktorá je určená parametricky x=5+t y=1+3t z=-2t t patri R a roviny, ktorá je určená všeobecnou rovnicou 2x-y+3z-4=0. - Koncových 73044
 Nájdite bod P na úsečke AB tak, že |AP| = r |AB| . Súradnice koncových bodov: A = (−2, 0, 1), B = (10, 8, 5), pomer r = 1/4.
Nájdite bod P na úsečke AB tak, že |AP| = r |AB| . Súradnice koncových bodov: A = (−2, 0, 1), B = (10, 8, 5), pomer r = 1/4. - Sú dané
 Sú dané body: A(-3, 1), B (2,-4), C ( 3, 3) a) Určite obvod trojuholníka ABC. b) Rozhodnite aký je trojuholník ABC. c) Určite dĺžku kružnice vpísanej
Sú dané body: A(-3, 1), B (2,-4), C ( 3, 3) a) Určite obvod trojuholníka ABC. b) Rozhodnite aký je trojuholník ABC. c) Určite dĺžku kružnice vpísanej - Vektory v priestore 3D
 Dané sú vektory u=(1;3;-4), v=(0;1;1). Určte veľkosť týchto vektorov, vypočitajte uhol vektorov, vzdialenosť medzi vektormi.
Dané sú vektory u=(1;3;-4), v=(0;1;1). Určte veľkosť týchto vektorov, vypočitajte uhol vektorov, vzdialenosť medzi vektormi. - Bod na priamke
 Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší.
Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší. - Kolmý priemet
 Určte vzdialenosť bodu B [1, -3] od kolmého priemetu bodu A [3, -2] na priamku 2 x + y + 1 = 0.
Určte vzdialenosť bodu B [1, -3] od kolmého priemetu bodu A [3, -2] na priamku 2 x + y + 1 = 0. - Vektor umiestnite
 Vektor AB, ale A(3,-1), B(5,3) umiestnite do bodu C(1,3) tak že, AB=CO
Vektor AB, ale A(3,-1), B(5,3) umiestnite do bodu C(1,3) tak že, AB=CO - Smernica
 Ktorá z funkcii je rastúca? a) y=2-x b) y=20 c) y=(x+2). (-5) d) y=x-2
Ktorá z funkcii je rastúca? a) y=2-x b) y=20 c) y=(x+2). (-5) d) y=x-2 - Trojuholník KLM
 Dané sú body K( -3; 2), L(-1; 4), M(3, -4). Zistite: a) či je trojuholník KLM pravouhlý b) vypočítajte dĺžku ťažnice na stranu k c) napíšte súradnice vektora LM d) napíšte smernicový tvar strany KM e) napíšte smernicový tvar osi strany KM
Dané sú body K( -3; 2), L(-1; 4), M(3, -4). Zistite: a) či je trojuholník KLM pravouhlý b) vypočítajte dĺžku ťažnice na stranu k c) napíšte súradnice vektora LM d) napíšte smernicový tvar strany KM e) napíšte smernicový tvar osi strany KM - Vektor v4
 Nájdite vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1)
Nájdite vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1) - Vzdialenosť
 Vypočítajte vzdialenosť bodu A [0, 2] od priamky prechádzajúcej bodmi B [9, 5] a C [1, -1].
Vypočítajte vzdialenosť bodu A [0, 2] od priamky prechádzajúcej bodmi B [9, 5] a C [1, -1]. - Dvanásťuholník
 Vypočítajte veľkosť menšieho z uhlov, ktorý určujú priamky A1 A4 a A2 A10 v pravidelnom dvanásťuholníku A1A2A3 . .. A12. Výsledok uveďte v stupňoch.
Vypočítajte veľkosť menšieho z uhlov, ktorý určujú priamky A1 A4 a A2 A10 v pravidelnom dvanásťuholníku A1A2A3 . .. A12. Výsledok uveďte v stupňoch. - Súradnice vrcholov
 Určte súradnice vrcholov a obsah rovnobeznika, ktoreho dve strany ležia na priamkach 8x+3y+1=0, 2x+y-1=0 a uhlopriečka na priamke 3x+ 2y+3=0
Určte súradnice vrcholov a obsah rovnobeznika, ktoreho dve strany ležia na priamkach 8x+3y+1=0, 2x+y-1=0 a uhlopriečka na priamke 3x+ 2y+3=0
