Rast populácie
Koľko ľudí bude na zemi z dvoch ľudí za 5000 rokov, ak sa narodia každému páru vždy vo veku 25-35 rokov 4 deti, 2x chlapec a 2x dievča a každý človek sa dožije 75rokov?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- geometrická postupnosť
- nekonečný geometrický rad
- vyjadrenie neznámej zo vzorca
- základné funkcie
- úvaha
- exponenciála
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Na školskom 6
 Na školskom výlete sa zúčastnilo 48 deti. Šiesti z nich tam boli spolu s jedným súrodencom, Deväť detí tam bolo s dvomi súrodencami a štyria s tromi súrodencami. Ostatní na výlete súrodencov nemali. Po návrate čakali na deti rodičia, aby ich odviezli auto
Na školskom výlete sa zúčastnilo 48 deti. Šiesti z nich tam boli spolu s jedným súrodencom, Deväť detí tam bolo s dvomi súrodencami a štyria s tromi súrodencami. Ostatní na výlete súrodencov nemali. Po návrate čakali na deti rodičia, aby ich odviezli auto - Spravodlivo 4
 Vnučka Mia pomahala starkej 3 dní, Ema 2 dní a Zoja 4 dní. V akom pomerne ma starká rozdeliť čokoládu medzi vnučky, ak ich chce spravodlivo odmeniť podľa toho, ako dlho jej pomáhali.?
Vnučka Mia pomahala starkej 3 dní, Ema 2 dní a Zoja 4 dní. V akom pomerne ma starká rozdeliť čokoládu medzi vnučky, ak ich chce spravodlivo odmeniť podľa toho, ako dlho jej pomáhali.? - Hod kockou 2
 Päťkrát hodíme kockou . Napíš: a) 3 udalosti ktoré určite nemôžu nastať. Pri každej napíš dôvod. b) 3 udalosti ktoré určite nastanú pri každej napísať dôvod. A ďalšia úloha je 3 udalosti ktoré môžu ale nemusia nastať pri každej napísať dôvod.
Päťkrát hodíme kockou . Napíš: a) 3 udalosti ktoré určite nemôžu nastať. Pri každej napíš dôvod. b) 3 udalosti ktoré určite nastanú pri každej napísať dôvod. A ďalšia úloha je 3 udalosti ktoré môžu ale nemusia nastať pri každej napísať dôvod. - Päť hostí
 Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba?
Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba?
- V debne
 V debne je 10 súčiastok, 3 z nich sú chybné. Vyberme náhodne 4 súčiastky. Aká je pravdepodobnosť, že medzi nimi bude a) 0 chybných, b) práve jedna chybná súčiastka, c) práve dve chybné súčiastky, d) práve 4 chybné súčiastky?
V debne je 10 súčiastok, 3 z nich sú chybné. Vyberme náhodne 4 súčiastky. Aká je pravdepodobnosť, že medzi nimi bude a) 0 chybných, b) práve jedna chybná súčiastka, c) práve dve chybné súčiastky, d) práve 4 chybné súčiastky? - Kosodĺžnik výšky
 Vypočítaj výšku kosodĺžnika ABCD na stranu BC, ak je AB=7cm, BC=5,5cm a výška prvej strany na AB=4,4cm
Vypočítaj výšku kosodĺžnika ABCD na stranu BC, ak je AB=7cm, BC=5,5cm a výška prvej strany na AB=4,4cm - Na výstave
 Na výstave bolo štyrikrát viac dievčat ako chlapcov. O koľko percent bolo na výstave viac dievčat ako chlapcov?
Na výstave bolo štyrikrát viac dievčat ako chlapcov. O koľko percent bolo na výstave viac dievčat ako chlapcov? - Traja 44
 Traja chlapci Ivo, Vlado a Alan čítajú tú istú knihu, pričom si dal podmienku, že počas celého čítania budú každý deň čítať vždy rovnaký počet strán, až kým knihu nedočítajú do konca. Ivo z nej denne prečíta 18 strán, Vlado 24 strán a Alan 20 strán. Overt
Traja chlapci Ivo, Vlado a Alan čítajú tú istú knihu, pričom si dal podmienku, že počas celého čítania budú každý deň čítať vždy rovnaký počet strán, až kým knihu nedočítajú do konca. Ivo z nej denne prečíta 18 strán, Vlado 24 strán a Alan 20 strán. Overt - Anna malá
 Anna mala 3 krát viac ako Beátka. Cilka mala o 2 eura viac ako Beátka. Spolu mali 52 eur. Koľko mala každá?
Anna mala 3 krát viac ako Beátka. Cilka mala o 2 eura viac ako Beátka. Spolu mali 52 eur. Koľko mala každá?
- Zamestnanci 4
 V sklade pracuje 21 zamestnancov - robotníkov a administratívnych pracovníkov. Pri úprave miezd znížili dennú odmenu každého administratívneho pracovníka o 3 € a dennú odmenu každého robotníka zvýšili o 2 €, takže celková denná mzda vzrástla o 17 €. Vypoč
V sklade pracuje 21 zamestnancov - robotníkov a administratívnych pracovníkov. Pri úprave miezd znížili dennú odmenu každého administratívneho pracovníka o 3 € a dennú odmenu každého robotníka zvýšili o 2 €, takže celková denná mzda vzrástla o 17 €. Vypoč - Jednotky, dvojky, trojky
 V triede je 30 žiakov. Piati mali známku trojku. Ostatní dvojky a jednotky. Priemer známok bol 1,9. Koľko žiakov malo jednotku?
V triede je 30 žiakov. Piati mali známku trojku. Ostatní dvojky a jednotky. Priemer známok bol 1,9. Koľko žiakov malo jednotku? - Nádoba - štvorsten
 Nádoba tvaru rotačného valca s polomerom podstavy 5 cm je naplnená vodou. O čo stúpne hladina vody v nádobe, ak do nej ponoríme pravidelný štvorsten s hranou 7cm.
Nádoba tvaru rotačného valca s polomerom podstavy 5 cm je naplnená vodou. O čo stúpne hladina vody v nádobe, ak do nej ponoríme pravidelný štvorsten s hranou 7cm. - Hodiny dekadické
 V republikánskom kalendári (používal sa vo Francúzsku v rokoch 1793 – 1805) bola doba jedného celého dňa rozdelená na 10 hodín, každá hodina mala 100 minút a každá minúta mala 100 sekúnd. Koľko by ukazovali vtedajšie hodiny v čase, keď dnešné hodiny ukazu
V republikánskom kalendári (používal sa vo Francúzsku v rokoch 1793 – 1805) bola doba jedného celého dňa rozdelená na 10 hodín, každá hodina mala 100 minút a každá minúta mala 100 sekúnd. Koľko by ukazovali vtedajšie hodiny v čase, keď dnešné hodiny ukazu - Na mobile
 PIN na mobile má 4 znaky. Aká je pravdepodobnosť, že PIN obsahuje číslo 7 a končí číslom 5?
PIN na mobile má 4 znaky. Aká je pravdepodobnosť, že PIN obsahuje číslo 7 a končí číslom 5?
- Pokladník 4
 Pokladník Samuel mal v pokladni spolu 20 ks bankoviek v celkovej hodnote 850 eur. Boli to iba 50 eurové a 20 eurové bankovky. Koľko kusov mal z každej bankovky?
Pokladník Samuel mal v pokladni spolu 20 ks bankoviek v celkovej hodnote 850 eur. Boli to iba 50 eurové a 20 eurové bankovky. Koľko kusov mal z každej bankovky? - Trojuholníkov 83111
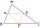 Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru - V triede 30
 V triede bolo 31 žiakov a aritmetický priemer hmotnosti bol 43 kg. Vypočítajte, aká bude priemerná hmotnosť v triede, ak do triedy pribudol žiak ťažký 91 kg.
V triede bolo 31 žiakov a aritmetický priemer hmotnosti bol 43 kg. Vypočítajte, aká bude priemerná hmotnosť v triede, ak do triedy pribudol žiak ťažký 91 kg.
