Pozorovateľ
Pozorovateľ vidí priamu ohradu dlhú 80 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 136 m.
Ako ďaleko je od druhého konca ohrady?
Ako ďaleko je od druhého konca ohrady?
Správna odpoveď:

Zobrazujem 1 komentár:
Anna
no obavam sa ze napokon cez sinusovu vetu to ma tiez dve riesenia...
vid aj https://www.hackmath.net/sk/priklad-uloha/24111?result=3
vid aj https://www.hackmath.net/sk/priklad-uloha/24111?result=3
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Chcete premeniť jednotku dĺžky?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Chcete premeniť jednotku dĺžky?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- rovnica
- aritmetika
- násobenie
- delenie
- planimetria
- trojuholník
- sínusová veta
- základné funkcie
- úmera, pomer
- čísla
- reálne čísla
- goniometria a trigonometria
- sínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Bod od roviny
 Vypočítaj vzdialenosť bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0
Vypočítaj vzdialenosť bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0 - Mama rozdelila
 Mama rozdelila štrúdľu svojim trom synom. Najprv odrezala 1/3 štrúdle. Zvyšok rozdelila v pomere 2:3. Rozdiel najdlhšieho a najkratšieho kúska je 4 cm. urč dĺžku štrúdle v cm
Mama rozdelila štrúdľu svojim trom synom. Najprv odrezala 1/3 štrúdle. Zvyšok rozdelila v pomere 2:3. Rozdiel najdlhšieho a najkratšieho kúska je 4 cm. urč dĺžku štrúdle v cm - 2x+3y-4=0 82676
 Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0.
Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0. - Vrcholy T3D
 Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A.
Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A. - Vypočítaj 425
 Vypočítaj, v akej vzdialenosti od osi otáčania pôsobí na jednej strane dvozvratnej páky sila 60N, ak na druhej strane pôsobí sila 180N vo vzdialenosti 1 meter od osi otáčania a páka je v rovnováhe
Vypočítaj, v akej vzdialenosti od osi otáčania pôsobí na jednej strane dvozvratnej páky sila 60N, ak na druhej strane pôsobí sila 180N vo vzdialenosti 1 meter od osi otáčania a páka je v rovnováhe - Ohnisko a priamka
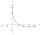 Určte rovnicu paraboly, ktorá má bod F = [3,2] za svoje ohnisko a priamku x+y+1=0 za svoju radiacu priamku.
Určte rovnicu paraboly, ktorá má bod F = [3,2] za svoje ohnisko a priamku x+y+1=0 za svoju radiacu priamku. - Určte 19
 Určte rovnicu kružnice, ktorá je množinou všetkých bodov roviny, ktoré majú od bodu [3,7] dvakrát väčšiu vzdialenosť ako od bodu [0,1].
Určte rovnicu kružnice, ktorá je množinou všetkých bodov roviny, ktoré majú od bodu [3,7] dvakrát väčšiu vzdialenosť ako od bodu [0,1]. - Trojuholníka 82144
 Vypočítajte veľkosť výšky na stranu b (v_b) trojuholníka ABC s vrcholmi A[4;1;3] B[2;3;3] a C[1;1;3].
Vypočítajte veľkosť výšky na stranu b (v_b) trojuholníka ABC s vrcholmi A[4;1;3] B[2;3;3] a C[1;1;3]. - Gotický
 Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice.
Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice. - Tetiva 22
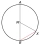 Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku?
Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku? - Nedisciplinovaný 80979
 Nedisciplinovaný motocyklista išiel po horskej ceste neprimeranou rýchlosťou, v zákrute nezvládol riadenie a pri rýchlosti 90 km. h‐1 opustil vozovku. Padal do strže s hĺbkou 36 m. Nakreslite obrázok rezu celou situáciou. Ako ďaleko motocykel dopadol a ak
Nedisciplinovaný motocyklista išiel po horskej ceste neprimeranou rýchlosťou, v zákrute nezvládol riadenie a pri rýchlosti 90 km. h‐1 opustil vozovku. Padal do strže s hĺbkou 36 m. Nakreslite obrázok rezu celou situáciou. Ako ďaleko motocykel dopadol a ak - Ako sa 3
 Ako sa predĺži koľajnica pri zmene teploty z -30°C na 30°C, ak je pri teplote 0°C dlhá 25 m? Teplotný koeficient dĺžkovej rozťažnosti je 12,10na-6Kna-1.
Ako sa predĺži koľajnica pri zmene teploty z -30°C na 30°C, ak je pri teplote 0°C dlhá 25 m? Teplotný koeficient dĺžkovej rozťažnosti je 12,10na-6Kna-1. - Poškodené
 Poškodené potrubie dĺžky 115m opravovali tri dni. Prvý deň opravili štvrtinu z toho čo druhý deň, tretí deň opravili o 20m menej ako druhý deň. Koľko m potrubia opravili v prvý, druhý, tretí deň?
Poškodené potrubie dĺžky 115m opravovali tri dni. Prvý deň opravili štvrtinu z toho čo druhý deň, tretí deň opravili o 20m menej ako druhý deň. Koľko m potrubia opravili v prvý, druhý, tretí deň? - Východiskového 80614
 Muž v púšti prejde 8,7 míle v smere S 26° W (juho-západ). Potom sa otočí o 90° a prejde 9 míľ v smere na N 49° W (severo západne). Ako ďaleko je v tom čase od svojho východiskového bodu a jeho postoj od jeho východiskového bodu?
Muž v púšti prejde 8,7 míle v smere S 26° W (juho-západ). Potom sa otočí o 90° a prejde 9 míľ v smere na N 49° W (severo západne). Ako ďaleko je v tom čase od svojho východiskového bodu a jeho postoj od jeho východiskového bodu? - Vzdialenosť 80542
 Nájdite na číselnej osi číslo, ktorého vzdialenosť od čísla 3 je štyrikrát menšia ako od čísla 15 (určte obe riešenia).
Nájdite na číselnej osi číslo, ktorého vzdialenosť od čísla 3 je štyrikrát menšia ako od čísla 15 (určte obe riešenia). - Aritmetickú 75124
 Dĺžky dvanástich pólov tvoria aritmetickú postupnosť (AP). Ak je tretí pól 3 m a ôsmy pól 5 m, nájdite (i) Dĺžka prvej tyče (ii) Súčet dĺžok tyčí
Dĺžky dvanástich pólov tvoria aritmetickú postupnosť (AP). Ak je tretí pól 3 m a ôsmy pól 5 m, nájdite (i) Dĺžka prvej tyče (ii) Súčet dĺžok tyčí - Obvod trojuholníka 3
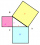 Urči obvod trojuholníka ABC kde bod A je začiatok súradnicovej sústavy, bod B je priesečník grafu linearnej funkcie f: y = - 3/4• x + 3 s osou x a C je priesečník grafu tejto funkcie s osou y.
Urči obvod trojuholníka ABC kde bod A je začiatok súradnicovej sústavy, bod B je priesečník grafu linearnej funkcie f: y = - 3/4• x + 3 s osou x a C je priesečník grafu tejto funkcie s osou y.
