Z9 – I – 5 MO 2018
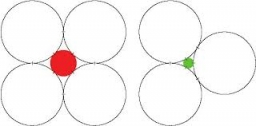
Peter a Ivan vytvárali dekorácie z navzájom zhodných bielych kruhov. Peter použil štyri kruhy, ktoré položil tak, že sa každý dotýkal dvoch iných kruhov. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých štyroch bielych kruhov, a ten vyfarbil červenou.
Ivan použil tri kruhy, ktoré položil tak, že sa dotýkali navzájom. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých troch bielych kruhov, a ten vyfarbil zelenou. Ivan si všimol, že jeho zelený kruh a Petrov červený kruh sú rôzne veľké, a tak začali spolu zisťovať, ako sa líšia.
Vyjadrite polomery červeného a zeleného kruhu všeobecne pomocou polomeru bielych kruhov.
Ivan použil tri kruhy, ktoré položil tak, že sa dotýkali navzájom. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých troch bielych kruhov, a ten vyfarbil zelenou. Ivan si všimol, že jeho zelený kruh a Petrov červený kruh sú rôzne veľké, a tak začali spolu zisťovať, ako sa líšia.
Vyjadrite polomery červeného a zeleného kruhu všeobecne pomocou polomeru bielych kruhov.
Správna odpoveď:
Zobrazujem 11 komentárov:
Uzivatelka
a) - stred malej kruznice lezi na uhlopriecke stvorca so stranou 2r
b) - stred malej kruznice lezi v rovnostrannom trojuholniku so stranou 2r v jeho tazisku... taznica = vyska. Tazisko lezi v 2/3 dlzky taznice (alebo v 1/3 dlzky taznice)
b) - stred malej kruznice lezi v rovnostrannom trojuholniku so stranou 2r v jeho tazisku... taznica = vyska. Tazisko lezi v 2/3 dlzky taznice (alebo v 1/3 dlzky taznice)
Dr Math
ano, mate pravdu, r1 bol omylom priemer cerveneho kruhu... cize 2r1.... opravili sme
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Tri čísla 8
 Tri čísla, ktoré tvoria aritmetickú postupnosť, majú súčet 30. Ak odčítame od prvého 5, od druhého 4 a tretie ponecháme, dostaneme geometrickú postupnosť. Urči členy AP aj GP.
Tri čísla, ktoré tvoria aritmetickú postupnosť, majú súčet 30. Ak odčítame od prvého 5, od druhého 4 a tretie ponecháme, dostaneme geometrickú postupnosť. Urči členy AP aj GP. - Slávkine čísla
 Slávka si napísala farebnými fixkami štyri rôzne prirodzené čísla: červené, modré, zelené a žlté. Keď červené číslo vydelí modrým, dostane ako neúplný podiel zelené číslo a žlté predstavuje zvyšok po tomto delení. Keď vydelí modré číslo zeleným, vyjde jej
Slávka si napísala farebnými fixkami štyri rôzne prirodzené čísla: červené, modré, zelené a žlté. Keď červené číslo vydelí modrým, dostane ako neúplný podiel zelené číslo a žlté predstavuje zvyšok po tomto delení. Keď vydelí modré číslo zeleným, vyjde jej - V hoteli 2
 V hoteli Holiday majú na každom poschodí rovnaký počet izieb. Izby sú číslované prirodzenými číslami postupne od prvého poschodia, žiadne číslo nie je vynechané a každá izba má iné číslo. Do hotela pricestovali traja turisti. Prvý sa ubytoval v izbe číslo
V hoteli Holiday majú na každom poschodí rovnaký počet izieb. Izby sú číslované prirodzenými číslami postupne od prvého poschodia, žiadne číslo nie je vynechané a každá izba má iné číslo. Do hotela pricestovali traja turisti. Prvý sa ubytoval v izbe číslo - MO Z9–I–3 - 2017
 Roboti Róbert a Hubert skladajú a rozoberajú mlynčeky na kávu. Pritom každý z nich mlynček zloží štyrikrát rýchlejšie, ako ho sám rozoberie. Keď ráno prišli do dielne, niekoľko mlynčekov už tam bolo zložených. O 7:00 začal Hubert skladať a Róbert rozobera
Roboti Róbert a Hubert skladajú a rozoberajú mlynčeky na kávu. Pritom každý z nich mlynček zloží štyrikrát rýchlejšie, ako ho sám rozoberie. Keď ráno prišli do dielne, niekoľko mlynčekov už tam bolo zložených. O 7:00 začal Hubert skladať a Róbert rozobera - Určte 7
 Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1 = 5, an = 320, sn = 635, n=?, q=?
Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1 = 5, an = 320, sn = 635, n=?, q=? - Konečná GP
 Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1=18, an=13122, sn=19674, n=?, q=?
Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1=18, an=13122, sn=19674, n=?, q=? - Geometrická 11
 Geometrická postupnosť so šiestimi členmi má súčet všetkých šiestich členov rovnajúci sa 63; súčet párnych členov má hodnotu 42. Určte tieto členy.
Geometrická postupnosť so šiestimi členmi má súčet všetkých šiestich členov rovnajúci sa 63; súčet párnych členov má hodnotu 42. Určte tieto členy. - Ak odpočítame
 Ak odpočítame od čísel 33, 45 a 63 to isté číslo, dostaneme tri za sebou idúce členy GP. Určte túto GP a vypočítajte jej piaty člen.
Ak odpočítame od čísel 33, 45 a 63 to isté číslo, dostaneme tri za sebou idúce členy GP. Určte túto GP a vypočítajte jej piaty člen. - V rotačnom 2
 V rotačnom valci je dané: povrch plášťa (bez podstáv) S= 96 cm² a objem V= 192 cm kubických. Výpočitajte polomer a výšku tohto valca.
V rotačnom valci je dané: povrch plášťa (bez podstáv) S= 96 cm² a objem V= 192 cm kubických. Výpočitajte polomer a výšku tohto valca. - V rotačnom
 V rotačnom valci je dané: povrch S= 96 cm² a objem V= 192 cm kubických. Výpočitajte jeho polomer a výšku.
V rotačnom valci je dané: povrch S= 96 cm² a objem V= 192 cm kubických. Výpočitajte jeho polomer a výšku. - Stenové uhlopriečky
 Ak sú stenové uhlopriečky kvádra x, y a z (diagonály), potom nájdite objem kvádra. Vyriešte pre x=1,3, y=1,2, z=1,1
Ak sú stenové uhlopriečky kvádra x, y a z (diagonály), potom nájdite objem kvádra. Vyriešte pre x=1,3, y=1,2, z=1,1 - Dve tetivy 3
 Vypočítajte dĺžku tetivy AB a k nej kolmej tetivy BC, ak tetiva AB je od stredu kružnice k vzdialená 4 cm a tetiva BC má vzdialenosť 8 cm.
Vypočítajte dĺžku tetivy AB a k nej kolmej tetivy BC, ak tetiva AB je od stredu kružnice k vzdialená 4 cm a tetiva BC má vzdialenosť 8 cm. - MO Z9-I-6 2019
 Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami.
Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami. - Matik - KSM
 V kuchárskej knihe od Mateja Matemakaka sa písalo: najväčší spoločný deliteľ gramáže múky a gramáže cukru je 15, najväčší spoločný deliteľ gramáže cukru a gramáže citrónovej kôry je 6, súčin gramáže cukru a gramáže citrónovej kôry je 1800, najmenší spoloč
V kuchárskej knihe od Mateja Matemakaka sa písalo: najväčší spoločný deliteľ gramáže múky a gramáže cukru je 15, najväčší spoločný deliteľ gramáže cukru a gramáže citrónovej kôry je 6, súčin gramáže cukru a gramáže citrónovej kôry je 1800, najmenší spoloč - V Kocúrkove - Z8-I-6 2019 MO
 V Kocúrkove používajú mince iba s dvoma hodnotami, ktoré sú vyjadrené v kocúrkovských korunách kladnými celými číslami. Pomocou dostatočného množstva takých mincí je možné zaplatiť akúkoľvek celočíselnú sumu väčšiu ako 53 kocúrkovských korún, a to presne
V Kocúrkove používajú mince iba s dvoma hodnotami, ktoré sú vyjadrené v kocúrkovských korunách kladnými celými číslami. Pomocou dostatočného množstva takých mincí je možné zaplatiť akúkoľvek celočíselnú sumu väčšiu ako 53 kocúrkovských korún, a to presne - GP tri členy
 Druhý a tretí člen geometrickej postupnosti sú 24 a 12(c+1) v tomto poradí. Za predpokladu, že súčet prvých troch členov postupnosti je 76, určite hodnotu c.
Druhý a tretí člen geometrickej postupnosti sú 24 a 12(c+1) v tomto poradí. Za predpokladu, že súčet prvých troch členov postupnosti je 76, určite hodnotu c. - Rovnica hyperboly
 Napíšte rovnicu hyperboly so stredom S[0;0], ktorá prechádza bodmi: A[5;3] B[8; -10]
Napíšte rovnicu hyperboly so stredom S[0;0], ktorá prechádza bodmi: A[5;3] B[8; -10]
